Exercices en Scheme
Christian Queinnec
Université Paris 6 --- Pierre et Marie Curie
LIP6, 4 place Jussieu, 75252 Paris Cedex -- France
Revision: 1.43
Ces exercices sont diffusés sous la licence FDL (pour
Free Documentation
License).
Bibliographie
Pour en savoir plus, je recommande principalement
[Huf96] puis [Cha96] comme ouvrages d'introduction.
[Que94] n'est à lire que pour parachever la formation. Pour
les américanophiles, on retiendra surtout les remarquables
[AS85] (la première édition a été traduite
en français mais la seconde édition en anglais est meilleure),
[ML95] et [HKK99], on pourra également s'intéresser
à [SF89], [FWH92], [FF96b] ou
[FF96a].
Pour qui a accès au réseau, de nombreuses informations sont
disponibles dont le Scheme Repository
. Cette
archive contient des programmes, des implantations (pour Unix, Mac ou
Windows), des documents, les FAQ Scheme et de multiples pointeurs sur
d'autres ressources Scheme voire Lisp.
Références
- [Abd90]
-
Habib Abdulrab.
De Common Lisp à la programmation objet.
Hermès, 1990.
- [AD96]
-
Laurent Arditi and Stéphane Ducasse.
La programmation : une approche fonctionnelle et récursive
avec Scheme.
Eyrolles, 1996.
ISBN 2-212-08915-5.
- [All78]
-
John Allen.
Anatomy of Lisp.
Computer Science Series. McGraw-Hill, 1978.
- [AS85]
-
Harold Abelson and Gerald Jay with Julie Sussman Sussman.
Structure and Interpretation of Computer Programs.
MIT Press, Cambridge, Mass., 1985.
- [Cay83]
-
Michel Cayrol.
Le Langage Lisp.
Cepadues Editions, Toulouse (France), 1983.
- [Cha96]
-
Jacques Chazarain.
Programmer avec Scheme, de la pratique à la théorie.
International Thomson Publishing, 1996.
- [Dyb87]
-
R. Kent Dybvig.
The Scheme Programming Language.
Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1987.
- [FF96a]
-
Daniel P Friedman and Matthias Felleisen.
The Little Schemer.
MIT Press, Cambridge MA, 1996.
- [FF96b]
-
Daniel P Friedman and Matthias Felleisen.
The Seasoned Schemer.
MIT Press, Cambridge MA, 1996.
- [FWH92]
-
Daniel P Friedman, Mitchell Wand, and Christopher Haynes.
Essentials of Programming Languages.
MIT Press, Cambridge MA and McGraw-Hill, 1992.
- [Gib85]
-
William Gibson.
Neuromancien.
Fictions. La découverte, Paris (France), 1985.
- [Gir85]
-
Jean-Jacques Girardot.
Les langages et les systèmes Lisp.
EDItests, Paris (France), 1985.
- [Hen80]
-
Peter Henderson.
Functional Programming, Application and Implementation.
International Series in Computer Science. Prentice-Hall, 1980.
- [HKK99]
-
Max Hailperin, Barbara Kaiser, and Karl Knight.
Concrete Abstractions, An Introduction to Computer Science Using
Scheme.
Brooks/Cole Publishing Company, a division of International Thomson
Publishing Inc, 1999.
ISBN 0-534-95211-9.
- [Hof85]
-
Douglas Hofstadter.
Gödel, Escher, Bach.
InterÉditions, 1985.
- [Huf96]
-
Jean-Michel Hufflen.
Programmation fonctionnelle en Scheme. De la conception à la
mise en oeuvre.
Masson, 1996.
- [Kes88]
-
Robert R. Kessler.
Lisp, Objects, and Symbolic Programming.
Scott, Foreman/Little, Brown College Division, Glenview, Illinois,
1988.
- [KR85]
-
Georges Kiremitdjian and Jean-Pierre Roy.
Lire Lisp, le langage de l'intelligence artificielle.
CEDIC-Nathan, 1985.
- [MAE+62]
-
John McCarthy, Paul W. Abrahams, Daniel J. Edwards, Timothy P. Hart, and
Michael I. Levin.
Lisp 1.5 programmer's manual.
Technical report, MIT Press, Cambridge, MA (USA), 1962.
- [ML95]
-
Vincent Manis and James J Little.
The Schematics of computation.
Prentice-Hall, 1995.
- [PJ87]
-
Simon L. Peyton-Jones.
The Implementation of Functional Programming Languages.
International Series in Computer Science. Prentice-Hall, 1987.
- [Pou85]
-
William Poundstone.
The Recursive Universe.
Oxford University Press, 1985.
- [Que82]
-
Christian Queinnec.
Langage d'un autre type : Lisp.
Eyrolles, Paris (France), 1982.
- [Que84]
-
Christian Queinnec.
Lisp mode d'emploi.
Eyrolles, Paris (France), 1984.
- [Que94]
-
Christian Queinnec.
Les langages Lisp.
InterÉditions, Paris (France), 1994.
- [Ray91]
-
Eric Raymond.
The New Hacker's Dictionary.
MIT Press, Cambridge MA, 1991.
With assistance and illustrations by Guy L. Steele Jr.
- [Rib69]
-
Daniel Ribbens.
Programmation non numérique : Lisp 1.5.
Monographies d'Informatique, AFCET, Dunod, Paris, 1969.
- [SF89]
-
George Springer and Daniel P. Friedman.
Scheme and the Art of Programming.
MIT Press and McGraw-Hill, 1989.
- [SJ93]
-
Emmanuel Saint-James.
La programmation appplicative (de LISP à la machine en
passant par le lambda-calcul).
Hermès, 1993.
- [Ste90]
-
Guy L. Steele, Jr.
Common Lisp, the Language.
Digital Press, Burlington MA (USA), 2nd edition, 1990.
- [Wer85]
-
Harald Wertz.
Lisp, une introduction à la programmation.
Masson, 1985.
- [WH88]
-
Patrick H Winston and Berthold K Horn.
Lisp.
Addison Wesley, third edition, 1988.
1 Premiers pas en Scheme
Où l'on découvrira la récursion simple, double ou
enveloppée ainsi que la définition de fonctions locales tout en
manipulant des listes plates, des arbres binaires et même des petits
entiers.
Toutes les fonctions, solutions des énoncés suivants, sont
définissables en moins de 10 lignes.
Exercice 1 : Écrire la factorielle.
Solution de l'exercice 1 :
;;;
(define (factorielle nombre)
(if (= nombre 1)
1
(* nombre (factorielle (- nombre 1))) ) )
Attention il n'y a pas de grand nombre en Scheme->C, aussi
mélange-t-il flottants et entiers. En Bigloo par contre, les petits
entiers sont tronqués de la même manière qu'en C. En DrScheme, les
grands nombres (ou bignum en jargon) et les rationnels sont
disponibles.
? (FACTORIELLE 12)
= 479001600
? (FACTORIELLE 13)
= -215430144
Exercice 2 : Écrire une fonction retournant la somme des n premiers
carrés. Par exemple:
? (SOMME-CARRES 5)
= 55
Solution de l'exercice 2 : Songez à bien présenter vos programmes!
;;;
(define (somme-carres n)
(if (= n 0)
0
(+ (* n n) (somme-carres (- n 1))) ) )
Exercice 3 : Concevoir la fonction compter qui prend un symbole-lettre et une
liste de symboles-lettres et
compte les occurrences de ce premier parmi ces derniers. Par exemple,
si poeme-pi vaut (Q U E J A I M E A F A I R E A P P R E N D R E U N N O M B R E U T I L E A U S A G E), alors:
? (COMPTER 'N POEME-PI)
= 3
Solution de l'exercice 3 :
;;;
(define (compter mot phrase)
(if (pair? phrase)
(+ (if (equal? mot (car phrase)) 1 0) ;
(compter mot (cdr phrase)) )
0 ) )
Exercice 4 : Concevoir la fonction decompter qui prend un symbole et une
expression et décompte toutes les occurrences de ce premier dans
cette dernière (quelque soit la profondeur de ces occurrences). Par
exemple:
? (DECOMPTER 'A '((A B) ((C A)) A))
= 3
? (DECOMPTER 'C '((A B) ((C A)) A))
= 1
Solution de l'exercice 4 : La programmation suivante use de Sexpressions vues comme des arbres
binaires. Ainsi ((a b) ((c a)) a) est vue comme:
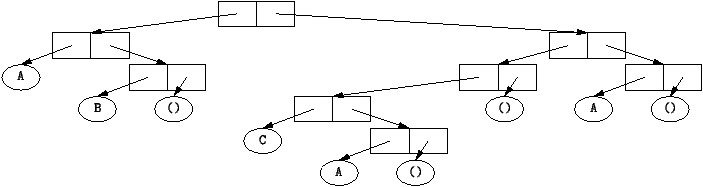
Voici la fonction:
;;;
(define (decompter feuille arbre)
(if (pair? arbre)
(+ (decompter feuille (car arbre)) ;
(decompter feuille (cdr arbre)) ) ;
(if (equal? feuille arbre)
1
0 ) ) )
Exercice 5 : Écrire la fonction begaie prenant une liste de symboles en
argument, une phrase, et retournant en sortie une phrase où tous les
mots sont répétés. Par exemple:
? (BEGAIE '(COMMENT ALLEZ VOUS))
= (COMMENT COMMENT ALLEZ ALLEZ VOUS VOUS)
Solution de l'exercice 5 :
(define (begaie phrase)
(if (pair? phrase) ;
(cons (car phrase) ;
(cons (car phrase) ;
(begaie (cdr phrase)) ) )
'() ) )
Exercice 6 : Écrire une fonction debegaie qui ôte d'une phrase tout
bégaiement et notamment celui produit par la fonction de l'exercice
précédent. Par exemple
? (DEBEGAIE (BEGAIE '(COMMENT ALLEZ VOUS)))
= (COMMENT ALLEZ VOUS)
Solution de l'exercice 6 :
(define (debegaie phrase)
(if (pair? phrase)
(if (pair? (cdr phrase))
(if (equal? (car phrase) ;
(cadr phrase) ) ;
(debegaie (cdr phrase))
(cons (car phrase) (debegaie (cdr phrase))) )
phrase )
phrase ) )
Notez que l'on ne saurait prendre le car ou le cdr d'un objet
que si l'on sait qu'il répond vrai à pair?. On ne peut donc
comparer le car et le cadr que si la liste contient au
moins deux termes.
Exercice 7 : Écrire la fonction impairs qui prend une liste de symboles
en argument et retourne la liste de tous les symboles de rang impair.
Par exemple:
? (IMPAIRS '(UN DEUX TROIS QUATRE))
= (UN TROIS)
? (IMPAIRS '(1 2 3 4 5))
= (1 3 5)
Solution de l'exercice 7 : Notez la récursion mutuelle entrecroisée:
;;;
(define (impairs liste)
(if (pair? liste)
(cons (car liste) (pairs (cdr liste)))
'() ) )
(define (pairs liste)
(if (pair? liste)
(impairs (cdr liste))
'() ) )
Notez que la notion de bégaiement n'est pas précise puisque des
mots répétés peuvent apparaître dans une phrase normale
comme (vous vous leurrez). En d'autres termes, la fonction
debegaie n'est pas l'inverse de la fonction begaie
tandis qu'impairs l'est.
On obtiendrait ainsi:
? (IMPAIRS (BEGAIE '(VOUS VOUS LEURREZ)))
= (VOUS VOUS LEURREZ)
? (DEBEGAIE (BEGAIE '(VOUS VOUS LEURREZ)))
= (VOUS LEURREZ)
Exercice 8 :
Concevoir la fonction aplatir qui prend une Sexpression en
argument et retourne la liste de tous les symboles qu'elle contient
dans l'ordre gauche-droite. Par exemple:
? (APLATIR '((A B) ((C))))
= (A B C)
? (APLATIR
(LIST (CONS 'A (CONS 'B 'C)) '((D B A) E)))
= (A B C D B A E)
Solution de l'exercice 8 : Là encore, on adopte la vision arbre binaire des Sexpressions.
(define (aplatir sexp)
(if (pair? sexp)
(append (aplatir (car sexp)) ;
(aplatir (cdr sexp)) )
(if (symbol? sexp)
(list sexp)
'() ) ) )
Exercice 9 : Concevoir une fonction prenant une Sexpression et retournant une forme
la calculant. Par exemple:
? (RECONSTRUIRE '(A B))
= (CONS 'A (CONS 'B '()))
Solution de l'exercice 9 : Merci à Annick Valibouze qui m'a transmis cette fonction issue du
folklore lointain de P6.
;;;
;;;
(define (reconstruire exp)
(if (pair? exp)
(list 'cons (reconstruire (car exp))
(reconstruire (cdr exp)) )
(list 'quote exp) ) )
Exercice 10 : Concevoir une fonction prenant un entier naturel en entrée et
retournant la liste de ses facteurs premiers. Un algorithme simple
suffira! Par exemple
? (FACTEURS-PREMIERS 625)
= (5 5 5 5)
? (FACTEURS-PREMIERS 123456)
= (2 2 2 2 2 2 3 643)
Solution de l'exercice 10 : Ceci est le premier exemple d'une sous-fonction définie localement.
;;;
(define (facteurs-premiers n)
(define (fp n essai)
(if (> n 1)
(if (= 0 (remainder n essai))
(cons essai (fp (quotient n essai) essai))
(fp n (+ 1 essai)) )
'() ) )
(if (= n 1) (list 1) (fp n 2)) )
On pourrait aussi écrire '(1) à la place de (list 1).
2 Toujours plus récursif!
Où de toujours plus complexes récursions sont proposées
au lecteur au fil de quelques catastrophes programmatiques.
Toutes les fonctions, solutions des énoncés suivants, sont
définissables en moins de vingt lignes.
À la recherche des doublons
Exercice 11 : Extraire d'une liste de symboles ceux qui y figurent au moins deux
fois. La réponse peut comporter des répétitions; son ordre est
inimportant. Rappelons que poeme-pi vaut
(Q U E J A I M E A F A I R E A P P R E N D R E U N N O M B R E U T I L E A U S A G E).
? (DOUBLONS POEME-PI)
= (U E A I M E A A I R E A P R E N R E U N E U E A)
Solution de l'exercice 11 :
;;;
(define (doublons liste)
(if (pair? liste)
(if (member (car liste) (cdr liste))
(cons (car liste) (doublons (cdr liste)))
(doublons (cdr liste)) )
'() ) )
;;;
(define (apparait-dans mot liste)
(and (pair? liste)
(or (equal? (car liste) mot)
(apparait-dans mot (cdr liste)) ) ) )
La fonction apparait-dans est prédéfinie en Scheme sous le
nom member. Une petite différence est que member
retourne #f ou le segment terminal de liste débutant par
l'élément recherché. On nomme member un semi-prédicat.
On peut aussi écrire (avec une variable tampon aussi appelé
accumulateur) mais on comparera les complexités relatives:
;;;
(define (doublons1 liste)
(define (parcourir liste deja-vus) ;
(if (pair? liste)
(if (apparait-dans (car liste) deja-vus)
(cons (car liste) (parcourir (cdr liste) deja-vus))
(parcourir (cdr liste) (cons (car liste) deja-vus)) )
'() ) )
(parcourir liste '()) )
Exercice 12 : Extraire d'une liste de symboles ceux qui y figurent exactement deux
fois. La réponse ne doit pas comporter de répétition mais son
ordre est inimportant.
? (STRICTS-DOUBLONS POEME-PI)
= (M P)
Solution de l'exercice 12 :
(define (stricts-doublons liste)
(define (parcourir liste deja-vus doublons trop-vus)
(if (pair? liste)
(cond ((member (car liste) trop-vus)
(parcourir (cdr liste) deja-vus doublons trop-vus) )
((member (car liste) doublons)
(parcourir (cdr liste) deja-vus
(retirer (car liste) doublons)
(cons (car liste) trop-vus) ) )
((member (car liste) deja-vus)
(parcourir (cdr liste) deja-vus
(cons (car liste) doublons) trop-vus ) )
(else
(parcourir (cdr liste) (cons (car liste) deja-vus)
doublons trop-vus ) ) )
doublons ) )
(parcourir liste '() '() '()) )
(define (retirer element liste)
(if (pair? liste)
(if (equal? element (car liste))
(cdr liste)
(cons (car liste) (retirer element (cdr liste))) )
'() ) )
On peut aussi écrire:
(define (stricts-doublons2 liste)
(if (pair? liste)
(let ((segment (member (car liste) (cdr liste))))
(if segment
(if (member (car liste) (cdr segment))
(stricts-doublons2 (retirer-tous (car liste) (cdr liste)))
(cons (car liste) (stricts-doublons2 (cdr liste))) )
(stricts-doublons2 (cdr liste)) ) )
'() ) )
(define (retirer-tous element liste)
(if (pair? liste)
(if (equal? element (car liste))
(retirer-tous element (cdr liste)) ;
(cons (car liste) (retirer-tous element (cdr liste))) )
'() ) )
Les résultats de stricts-doublons et stricts-doublons1
ne sont pas comparables. Il faut les comparer avec set-equal?.
(define (set-equal? set1 set2)
(define (set-included? set1 set2)
(if (pair? set1)
(and (member (car set1) set2)
(set-included? (cdr set1) set2) )
#t ) )
(and (set-included? set1 set2)
(set-included? set2 set1) ) )
Exercice 13 : Extraire d'un arbre binaire de symboles tous ceux qui y figurent
exactement deux fois.
? (EXTRAIRE-STRICTS-DOUBLONS
'((Q U
E
(J A I M E)
((A) F A I R E)
A
P
P
R
E
N
D
R
E)
((U N) ((N O M B R E) (U T I L E (A U))) S A G E)))
= (M P)
Solution de l'exercice 13 : On peut écrire ce qui suit qui use d'un style dit par continuations.
;;;
(define (extraire-stricts-doublons arbre)
(define (parcourir arbre deja-vus doublons trop-vus suite)
(if (pair? arbre)
(parcourir (car arbre)
deja-vus
doublons
trop-vus
(lambda (deja-vus doublons trop-vus)
(parcourir (cdr arbre)
deja-vus
doublons
trop-vus
suite ) ) )
(if (member arbre deja-vus)
(if (member arbre trop-vus)
(suite deja-vus doublons trop-vus)
(if (member arbre doublons)
(suite deja-vus (retirer arbre doublons)
(cons arbre trop-vus) )
(suite deja-vus (cons arbre doublons) trop-vus) ) )
(suite (cons arbre deja-vus) doublons trop-vus) ) ) )
(parcourir arbre '() '() '() (lambda (deja-vus doublons trop-vus)
doublons )) )
On peut aussi écrire, sans trop se fatiguer:
;;;
(define (extraire-stricts-doublons2 arbre)
(stricts-doublons (aplatir arbre)) )
Interlude
Exercice 14 : Concevoir une nouvelle fonction aplatir2 semblable à
l'aplatir de l'exercice 8 mais utilisant une
sous-fonction dotée d'un accumulateur.
Solution de l'exercice 14 :
(define (aplatir2 e)
(define (aplatir-interne e r)
(if (pair? e)
(aplatir-interne (car e) (aplatir-interne (cdr e) r))
(if (null? e) r (cons e r)) ) )
(aplatir-interne e '()) )
Exercice 15 : Concevoir la fonction xpl qui prend une liste de symboles et
retourne la liste de tous ses préfixes non vides en ordre croissant. Par
exemple:
? (XPL '(A B C))
= ((A) (A B) (A B C))
Solution de l'exercice 15 : Il y a des tas de façons d'écrire cette fonction. Voici deux styles:
(define (xpl liste)
(define (map-on-all-cdr fonction liste)
(if (pair? liste)
(cons (fonction liste)
(map-on-all-cdr fonction (cdr liste)) )
'() ) )
(reverse (map-on-all-cdr reverse (reverse liste))) )
(define (xpl1 l)
(define (xpl2 l l1)
(if (null? l) l1
(xpl2 (cdr l) (map (lambda (u) (cons (car l) u)) (cons '() l1)))))
(xpl2 (reverse l) '()))
Exercice 16 : Écrire la fonction reduce telle que
(reduce f e '(e1 e2 ...en)) calcule
(f 'e1 (f 'e2 ...(f 'en e) ...)).
Par exemple:
? (REDUCE * 1 '(1 2 3 4 5 6))
= 720
? (REDUCE
(LAMBDA (ELEMENT RESULTAT)
(APPEND RESULTAT (LIST ELEMENT)))
'()
'(A B C D))
= (D C B A)
Solution de l'exercice 16 :
(define (reduce fonction neutre liste)
(if (pair? liste)
(fonction (car liste) (reduce fonction neutre (cdr liste)))
neutre ) )
Exercice 17 : Utiliser la précédente fonction reduce pour définir la
fonction prédéfinie map ou même (très très
inefficacement) la factorielle de naguère (à l'aide de iota vue en cours).
Solution de l'exercice 17 :
(define (map-car fonction liste)
(reduce (lambda (x r) (cons (fonction x) r)) '() liste) )
(define (fact-orielle n)
(reduce * 1 (map-car (lambda (n) (+ n 1))
(iota 0 n) )) )
(define (iota debut fin)
(if (< debut fin)
(cons debut (iota (+ debut 1) fin))
'() ) )
Le filtrage
Exercice 18 : Le filtrage est une activité importante en Lisp (ou en ML) qui consiste à
vérifier si une expression est conforme à un filtre. Le filtre est
une description simple décrivant la forme que doit revêtir une
expression pour être acceptable ou filtrée avec succès.
On considère pour l'instant des listes de symboles (ou listes
linéaires). Un filtre sera une liste de filtres élémentaires
c'est-à-dire soit un symbole, soit un trou élémentaire noté
?-. Le filtre (foo ?- bar) accepte toute expression de
trois termes dont le premier est le symbole foo et le dernier,
le symbole bar. Le second peut être n'importe quoi.
Programmer cette fonction filtrer1 dont voici quelques
exemples:
? (FILTRER1 '(FOO) '(FOO ?- BAR))
= #F
? (FILTRER1 '(FOO BAR BAR) '(FOO ?- BAR))
= #T
? (FILTRER1 '(FOO HUX BAR WIX) '(FOO ?- BAR))
= #F
? (FILTRER1 '(FOO HUX BAR WIX) '(FOO ?- BAR ?-))
= #T
Solution de l'exercice 18 :
;;;
(define (filtrer1 expression filtre)
(if (pair? filtre)
(and (pair? expression)
(if (equal? (car filtre) '?-)
(filtrer1 (cdr expression) (cdr filtre))
(and (equal? (car expression) (car filtre))
(filtrer1 (cdr expression) (cdr filtre)) ) ) )
(null? expression) ) )
Exercice 19 : Un nouveau filtre est créé, le trou extensible, noté ...,
qui peut accepter un nombre quelconque de termes. Ainsi
le filtre (foo ... bar) accepte-t-il toute liste débutant par
foo et s'achevant par bar.
? (FILTRER2 '(FOO BAR) '(FOO ... BAR))
= #T
? (FILTRER2 '(FOO HUX BAR) '(FOO ... BAR))
= #T
? (FILTRER2 '(FOO HUX BAR WIX BAR) '(FOO ... BAR))
= #T
? (FILTRER2 '(FOO HUX BAR WIX BACH) '(FOO ... BAR))
= #F
? (FILTRER2
'(FOO HUX BAR WIX BACH)
'(FOO ... BAR ...))
= #T
Solution de l'exercice 19 :
;;;
(define (filtrer2 expression filtre)
(if (pair? filtre)
(cond ((equal? (car filtre) '?-)
(and (pair? expression)
(filtrer2 (cdr expression) (cdr filtre)) ) )
((equal? (car filtre) '...)
(or (filtrer2 expression (cdr filtre))
(and (pair? expression)
(filtrer2 (cdr expression) filtre) ) ) )
(else
(and (pair? expression)
(equal? (car expression) (car filtre))
(filtrer2 (cdr expression) (cdr filtre)) ) ) )
(null? expression) ) )
Exercice 20 :
On ne restreint plus maintenant les expressions à des listes
linéaires de symboles, parallèlement
les filtres pourront contenir eux-mêmes des
sous-filtres. Concevoir donc une nouvelle fonction filtrer3
capable de filtrer des arbres binaires avec des trous ?- et des
trous .... Par exemple:
? (FILTRER3 '(X (Y)) '((FOO ...) ?- (... BAR)))
= #F
? (FILTRER3
'((FOO BAR) (FOO BAR) (FOO BAR))
'((FOO ...) ?- (... BAR)))
= #T
Solution de l'exercice 20 :
;;;
(define (filtrer3 expression filtre)
(define (filtrer3-liste expressions filtres)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(or (filtrer3-liste expressions (cdr filtres))
(and (pair? expressions)
(filtrer3-liste (cdr expressions) filtres) ) )
(and (pair? expressions)
(filtrer3 (car expressions) (car filtres))
(filtrer3-liste (cdr expressions) (cdr filtres)) ) )
(equal? expressions filtres) ) )
(or (equal? filtre '?-)
(if (equal? filtre '...)
(error 'filtrer3 "... ne peut survenir ici")
(if (pair? filtre)
(filtrer3-liste expression filtre)
(equal? expression filtre) ) ) ) )
3 Fonctionnelles
Où l'on verra à l'oeuvre des fonctions manipulant des
fonctions et en synthétisant de nouvelles.
Exercice 21 : Concevoir une représentation fonctionnelle des listes
d'associations. Une première fonction représente la A-liste vide,
une seconde permet d'étendre une A-liste avec un nouveau couple,
enfin on peut scruter une A-liste par sa représentation même.
Par exemple:
? (DEFINE AL (NULL-A-LISTE))
= AL
? (SET! AL (EXTEND-A-LISTE AL 'ONE 1))
? (SET! AL (EXTEND-A-LISTE AL 'ZERO 0))
? (AL 'ONE)
= 1
? ((EXTEND-A-LISTE AL 'ONE 10) 'ONE)
= 10
Solution de l'exercice 21 :
;;;
(define (null-A-liste)
(lambda (element) #f) )
(define (extend-A-liste al clef valeur)
(lambda (element)
(if (equal? clef element)
valeur
(al element) ) ) )
Exercice 22 : Modifier la représentation précédente pour que la propriété
(eq? (null-A-liste) (null-A-liste)) soit vraie.
Solution de l'exercice 22 : On met simplement en facteur le résultat qui est une fonction
n'enclosant aucune variable libre.
(define null-A-liste-commune
(let ((f (lambda (element) #f)))
(lambda () f) ) )
Variations autour de composition
Exercice 23 : Définir la fonction compose qui prend deux fonctions (disons
f et g) en arguments et retourne la fonction unaire appliquant f
puis g. Par exemple:
? (DEFINE KADR (COMPOSE CDR CAR))
= KADR
? (KADR '(A B C))
= B
Solution de l'exercice 23 :
(define (compose f g)
(lambda (x) (g (f x))) )
Exercice 24 : Étendre la fonction compose pour composer une fonction f
prenant un nombre quelconque d'arguments avec une fonction unaire g.
Par exemple:
? (DEFINE LIST-LENGTH (NCOMPOSE LIST LENGTH))
= LIST-LENGTH
? (LIST-LENGTH 1 'B "c")
= 3
Solution de l'exercice 24 :
(define (ncompose f g)
(lambda arguments
(g (apply f arguments)) ) )
Exercice 25 : Étendre encore la fonction compose pour composer un nombre
quelconque de fonctions unaires. Par exemple:
? (DEFINE KADDDR (COMPOSE-N CDR CDR CDR CAR))
= KADDDR
? (KADDDR '(A B C D E))
= D
Solution de l'exercice 25 :
(define (compose-n . fns)
(lambda (x)
((reduce compose (lambda (x) x) fns) x) ) )
Discrétisation et extension de domaine
Exercice 26 :
Il est parfois utile, dans les jeux vidéos, de pouvoir calculer
rapidement des lignes trigométriques. Une façon simple de faire
est de précalculer (tabuler) les lignes dont on aura besoin. On
utilisera des vecteurs pour représenter ces tables et non les
Alistes précédentes.
Écrire la fonctionnelle faire-sinus qui prend en argument le pas
de discrétisation et retourne une fonction équivalente à sinus,
cette dernière retournera pour tout nombre le sinus précalculé
approché. Pour simplifier, on supposera que les nombres dont on
prend le sinus sont compris entre 0 et p/2. L'exemple suivant
discrétise la fonction sinus en 5 intervalles, soit 6 valeurs.
? (DEFINE SINUS1 (FAIRE-SINUS 5))
= SINUS1
? (SINUS1 0)
= 0.0
? (SINUS1 (/ PI 8))
= 0.30901699436641
? (SINUS1 (/ PI 5))
= 0.58778525227794
? (SINUS1 (/ PI 4))
= 0.58778525227794 ;
? (SINUS1 (/ PI 3))
= 0.80901699435911
? (SINUS1 (/ PI 2))
= 1.0
? (DESSINER SINUS1 0 (/ PI 2) (/ PI 10) 0 1 40)* 0=>0.0
* 0.31415926535=>0.30901699436641
* 0.6283185307=>0.58778525227794
* 0.94247779605=>0.80901699435911
* 1.2566370614=>0.95105651628405
* 1.57079632675=>1.0
= #<a Function>
La fonction dessiner sera demandée à l'exercice 29.
Solution de l'exercice 26 :
(define (faire-sinus nombre)
(let ((pas (/ pi (* 2 nombre)))
(table (make-vector (+ nombre 1) 0.0)) )
(do ((i 0 (+ 1 i)))
((>= i nombre) (vector-set! table nombre 1.0))
(vector-set! table i (sin (* pas i))) )
(lambda (x)
(vector-ref table (inexact->exact (floor (/ x pas)))) ) ) )
Exercice 27 : La fonction sinus précédente n'était valide qu'entre 0 et
p/2. Concevez une fonctionnelle prenant une fonction définie sur
un intervalle [a ... b[ et l'étendant à la manière d'un
sinus sur un intervalle quatre fois plus grand.
Voici un exemple sur une rampe linéaire.
? (DEFINE F4 (ETENDRE (LAMBDA (X) (- X)) 0 1))
= F4
? (DESSINER F4 0 4 (/ 1 5) -1 1 40) * 0=>0
* 0.2=>-0.2
* 0.4=>-0.4
* 0.6=>-0.6
* 0.8=>-0.8
* 1.0=>-1.0
* 1.2=>-0.8
* 1.4=>-0.6
* 1.6=>-0.4
* 1.8=>-0.2
* 2.0=>-2.2204460492503e-16
* 2.2=>0.2
* 2.4=>0.4
* 2.6=>0.6
* 2.8=>0.8
* 3.0=>1.0
* 3.2=>0.8
* 3.4=>0.6
* 3.6=>0.4
* 3.8=>0.2
= #<a Function>
Solution de l'exercice 27 :
(define (etendre fonction debut fin)
(let* ((empan (- fin debut))
(deux-empans (* 2 empan))
(milieu (+ fin empan)) )
(lambda (x)
(if (< x milieu)
(if (< x fin)
(fonction x)
(fonction (- milieu x)) )
(if (< x (+ milieu empan))
(- (fonction (- x milieu)))
(- (fonction (- (+ milieu deux-empans) x))) ) ) ) ) )
Exercice 28 : Un dernier effort suffira maintenant à rendre sinus1 apte à prendre
tout nombre flottant. Concevoir une fonctionnelle prenant une fonction
périodique définie sur un intervalle et retournant une nouvelle
fonction définie partout. Par exemple:
? (DEFINE SINUS
(ITERER (ETENDRE SINUS1 0 (/ PI 2)) 0 (* 2 PI)))
= SINUS
? (SINUS (- (/ PI 4)))
= -0.58778525227794
? (SINUS (- (/ PI 4) (* 6 PI)))
= 0.58778525227794
? (DESSINER SINUS 0 (* 3 PI) (/ PI 10) -1 1 40) * 0=>0.0
* 0.31415926535=>0.30901699436641
* 0.6283185307=>0.58778525227794
* 0.94247779605=>0.80901699435911
* 1.2566370614=>0.95105651628405
* 1.57079632675=>1.0
* 1.8849555921=>0.95105651628405
* 2.19911485745=>0.80901699435911
* 2.5132741228=>0.58778525227794
* 2.82743338815=>0.30901699436641
* 3.1415926535=>0.0
* 3.45575191885=>0.0
* 3.7699111842=>-0.30901699436641
* 4.08407044955=>-0.58778525227794
* 4.3982297149=>-0.80901699435911
* 4.71238898025=>-0.95105651628405
* 5.0265482456=>-0.95105651628405
* 5.34070751095=>-0.80901699435911
* 5.6548667763=>-0.58778525227794
* 5.96902604165=>-0.30901699436641
* 6.283185307=>0.0
* 6.59734457235=>0.0
* 6.9115038377=>0.30901699436641
* 7.22566310305=>0.58778525227794
* 7.5398223684=>0.80901699435911
* 7.85398163375=>0.95105651628405
* 8.1681408991=>0.95105651628405
* 8.48230016445=>0.80901699435911
* 8.7964594298=>0.58778525227794
* 9.11061869515=>0.30901699436641
* 9.4247779605=>0.0
= #<a Function>
Solution de l'exercice 28 :
(define (iterer fonction debut fin)
(let ((empan (- fin debut)))
(lambda (x)
(let* ((f (/ (- x debut) empan))
(r (- (- x debut) (* (floor f) empan))) )
(fonction r)) ) ) )
Exercice 29 :
Écrire une fonction dessinant sinus et autres fonctions de ce
genre. On pourra s'inspirer de la fonction dessiner des exemples
précédents. Elle a pour interface:
(define (dessiner fonction ;
;;
debut ;
fin ;
pas ;
;;
min ;
max ;
ligne ;
) ... )
Solution de l'exercice 29 :
(define (dessiner fonction debut fin pas min max ligne)
(define (display-star y)
(let ((n (inexact->exact (* ligne (/ (- y min) (- max min))))))
(do ((i 0 (+ 1 i)))
((> i ligne)(display " "))
(if (= i n) (display "*") (display " ")) ) ) )
(do ((x debut (+ x pas)))
((> x fin) fonction)
(let ((y (fonction x)))
(display-star y)
;;
(display x)
(display "=>")
(display y)
(newline) ) ) )
Exercice 30 : Plutôt que d'avoir écrit faire-sinus, comme à l'exercice
26, et parce que l'on
dispose de la fonction prédéfinie sin, on pourrait
écrire une fonction de discrétisation. Par exemple:
? (DEFINE SINUS0 (DISCRETISER SIN 0 (/ PI 2) 10))
= SINUS0
? (DESSINER SINUS0 0 (/ PI 2) (/ PI 30) 0 1 40)* 0=>0.0
* 0.10471975511667=>0.0
* 0.20943951023333=>0.1564344650358
* 0.31415926535=>0.30901699436641
* 0.41887902046667=>0.30901699436641
* 0.52359877558333=>0.45399049972755
* 0.6283185307=>0.58778525227794
* 0.73303828581667=>0.58778525227794
* 0.83775804093333=>0.70710678117067
* 0.94247779605=>0.80901699435911
* 1.0471975511667=>0.80901699435911
* 1.1519173062833=>0.8910065241741
* 1.2566370614=>0.95105651628405
* 1.3613568165167=>0.95105651628405
* 1.4660765716333=>0.98768834058882
= #<a Function>
Redéfinir alors faire-sinus avec discretiser.
Solution de l'exercice 30 :
(define (discretiser fonction debut fin nombre)
(let ((pas (/ (- fin debut) nombre))
(table (make-vector (+ nombre 1) 0.0)) )
(do ((i 0 (+ 1 i)))
((>= i nombre))
(vector-set! table i (fonction (+ debut (* pas i)))) )
(vector-set! table nombre (fonction fin))
(lambda (x)
(vector-ref table (inexact->exact (floor (/ (- x debut) pas)))) ) ) )
On remarquera que faire-sinus peut se redéfinir avec
discretiser.
(define (faire-sinus-avec-discretiser nombre)
(discretiser sin 0 (/ pi 2) nombre) )
Exercice 31 : Plutôt que d'indiquer le pas de discrétisation, autant le faire
calculer pour que l'erreur n'excède pas une certaine valeur.
Écrire la fonction discretiser2 telle que dans l'exemple
suivant l'erreur de discrétisation soit inférieure à 1/10.
? (DEFINE SINUS00
(ITERER
(ETENDRE
(DISCRETISER2 SIN 0 (/ PI 2) (/ 1 10))
0
(/ PI 2))
0
(* 2 PI)))
= SINUS00
? (DESSINER SINUS00 0 (/ PI 2) (/ PI 31) 0 1 40)* 0=>0.0
* 0.1013416985=>0.098017140326768
* 0.202683397=>0.19509032201062
* 0.3040250955=>0.29028467724641
* 0.405366794=>0.38268343235472
* 0.5067084925=>0.47139673681362
* 0.608050191=>0.5555702330056
* 0.7093918895=>0.63439328414846
* 0.810733588=>0.70710678117067
* 0.9120752865=>0.77301045334672
* 1.013416985=>0.83146961228696
* 1.1147586835=>0.8819212643338
* 1.216100382=>0.9238795324984
* 1.3174420805=>0.95694033572162
* 1.418783779=>0.98078528039557
* 1.5201254775=>0.99518472666807
= #<a Function>
Solution de l'exercice 31 : Seize pas sufffisent pour sinus00.
(define (discretiser2 fonction debut fin erreur)
(let essayer ((nombre-de-pas 2))
(let ((df (discretiser fonction debut fin nombre-de-pas))
(pas (/ (- fin debut) nombre-de-pas)) )
(define (verifier-erreur i fi)
(or (>= i fin)
(let* ((i+1 (+ i pas))
(fi+1 (df i+1)) )
(and (<= (abs (- fi+1 fi)) erreur)
(verifier-erreur i+1 fi+1) ) ) ) )
(if (verifier-erreur debut (df debut))
df
(essayer (+ nombre-de-pas 1)) ) ) ) )
Exercice 32 : La fonction cosinus n'est guère qu'un sinus décalé
de p/2, ce que l'on pourrait écrire:
? (DEFINE COSINUS (DECALER SINUS00 (/ PI 2)))
= COSINUS
? (DESSINER COSINUS 0 (* 2 PI) (/ PI 10) -1 1 40) * 0=>1.0
* 0.31415926535=>0.9238795324984
* 0.6283185307=>0.77301045334672
* 0.94247779605=>0.5555702330056
* 1.2566370614=>0.29028467724641
* 1.57079632675=>0.0
* 1.8849555921=>-0.29028467724641
* 2.19911485745=>-0.5555702330056
* 2.5132741228=>-0.77301045334672
* 2.82743338815=>-0.9238795324984
* 3.1415926535=>-0.99518472666807
* 3.45575191885=>-0.9238795324984
* 3.7699111842=>-0.77301045334672
* 4.08407044955=>-0.5555702330056
* 4.3982297149=>-0.29028467724641
* 4.71238898025=>0.0
* 5.0265482456=>0.29028467724641
* 5.34070751095=>0.5555702330056
* 5.6548667763=>0.77301045334672
* 5.96902604165=>0.9238795324984
* 6.283185307=>0.99518472666807
= #<a Function>
Écrire la fonctionnelle permettant de passer de sinus à cosinus.
Solution de l'exercice 32 :
(define (decaler fonction delta)
(lambda (x)
(fonction (+ x delta)) ) )
Mémo-fonctions et anté-mémoires
Exercice 33 : Il se peut qu'un même calcul soit demandé plusieurs fois de
suite. Concevoir donc une fonctionnelle prenant en argument une
fonction unaire et memorisant le dernier résultat calculé par
cette fonction unaire. Si celui-ci est redemandé, on retournera
alors ce résultat sans recalcul. On nomme cette technique memoization ou mémo-fonction. Appliquons-la à la fonction
member sur une longue liste que l'on bâtira avec
(define (faire-longue-liste element fin longueur)
(if (> longueur 0)
(faire-longue-liste element (cons element fin) (- longueur 1))
fin ) )
? (DEFINE UNE-LONGUE-LISTE
(FAIRE-LONGUE-LISTE 'FOO '(BAR HUX) 100000))
= UNE-LONGUE-LISTE ;
? (DEFINE CHERCHER
(MEMO (LAMBDA (X) (MEMBER X UNE-LONGUE-LISTE))))
= CHERCHER
? (CHERCHER 'BAR)
= (BAR HUX) ;
? (CHERCHER 'BAR)
= (BAR HUX) ;
Solution de l'exercice 33 :
;;;
(define (memo f)
(let ((au-moins-un-resultat #f)
(dernier-argument #f)
(dernier-resultat #f) )
(lambda (x)
(if (and au-moins-un-resultat (equal? x dernier-argument) )
dernier-resultat
(let ((resultat (f x)))
(set! dernier-argument x)
(set! dernier-resultat resultat)
(set! au-moins-un-resultat #t)
resultat ) ) ) ) )
Exercice 34 : Un cache de profondeur 1 peut ne pas être assez grand pour être
utile. Modifier la solution précédente afin de procurer une plus
grande profondeur de mémorisation. Par exemple: on peut modifier
chercher pour mémoriser les quatre dernières valeurs ayant
servi.
? (DEFINE CHERCHER4
(CACHE (LAMBDA (X) (MEMBER X UNE-LONGUE-LISTE))
4))
= CHERCHER4
? (CHERCHER4 'BAR)
= (BAR HUX) ;
? (CHERCHER4 'HUX)
= (HUX) ;
? (CHERCHER4 'BAR)
= (BAR HUX) ;
Solution de l'exercice 34 : Ce qui suit n'est pas une implantation de la technique dite LRU pour
``least recently used'' où l'on jette du cache la valeur qui a le
moins récemment servi.
(define (cache f taille)
(let ((arguments (make-vector taille #f))
(resultats (make-vector taille #f))
(libre 0) )
(define (echanger i j)
(let ((a (vector-ref arguments i))
(r (vector-ref resultats i)) )
(vector-set! arguments i (vector-ref arguments j))
(vector-set! resultats i (vector-ref resultats j))
(vector-set! arguments j a)
(vector-set! resultats j r)
r ) )
(define (memoriser x i)
(let ((r (f x)) )
(vector-set! arguments i x)
(vector-set! resultats i r)
r ) )
(lambda (x)
(let scruter ((i 0))
(if (>= i libre)
;;
(if (< libre taille)
(let ((i libre))
(set! libre (+ 1 libre))
(memoriser x i) )
(memoriser x (- taille 1)) )
(if (equal? (vector-ref arguments i) x)
;;
(echanger i 0)
(scruter (+ i 1)) ) ) ) ) ) )
Voici une autre solution due à Bruno Salvy.
;;;
(define (cache2 f taille)
(let* ((init (cons #t #f))
(lastargval (vector->list (make-vector taille (cons init init)))) )
(lambda (x)
(let ((found (assoc x lastargval)))
(if found (cdr found)
(begin (set! found (f x))
(set! lastargval (append! (cdr lastargval)
(list (cons x found))))
found ) ) ) ) ) )
4 Génération
Où programmes se transmuteront en compilateurs et
compilateurs en psychologues.
Le filtrage: le retour
Exercice 35 : Plutôt que d'être interprété par la fonction filtrer3
(cf. exercice 20).
le filtre (foo ?- bar) pourrait être transformé en une
fonction réalisant le même effet. On demande donc de réaliser
une curryfication de filtrer3 sur son filtre.
Par exemple:
? (TRANSFORMER-FILTRE5 '(FOO ?- BAR ... HUX))
= #<a Function>
? ((TRANSFORMER-FILTRE5 '(FOO ?- BAR ... HUX))
'(FOO 5 BAR HUX))
= #T
? ((TRANSFORMER-FILTRE5 '(FOO ?- BAR ... HUX))
'(FOO 5 BAR 7 4 5 HUX))
= #T
? ((TRANSFORMER-FILTRE5 '(FOO ?- BAR ... HUX))
'(FOO . BAR))
= #F
On évitera la banale solution suivante au profit d'une solution plus
efficace:
(define (filtrer3-curryfiee filtre)
(lambda (expression)
(filtrer3 expression filtre) ) )
Solution de l'exercice 35 :
;;;
(define (transformer-filtre5 filtre)
(define (transformer-liste filtres)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(let ((filtre-cdr (transformer-liste (cdr filtres))))
(letrec ((filtre
(lambda (expressions)
(or (filtre-cdr expressions)
(and (pair? expressions)
(filtre (cdr expressions)) ) ) ) ) )
filtre ) )
(let ((filtre-car (transformer-filtre5 (car filtres)))
(filtre-cdr (transformer-filtre5 (cdr filtres))) )
;;
(lambda (expressions)
(and (pair? expressions)
(filtre-car (car expressions))
(filtre-cdr (cdr expressions)) ) ) ) )
(lambda (expressions) (equal? expressions filtres)) ) )
(if (equal? filtre '?-)
(lambda (expression) #t)
(if (equal? filtre '...)
(lambda (expression)
(error 'transformer-filtre5 "... ne peut survenir ici") )
(if (pair? filtre)
(transformer-liste filtre)
(lambda (expression) (equal? filtre expression)) ) ) ) )
Exercice 36 : Plutôt que d'être interprété par la fonction
filtrer3, le filtre
(foo ?- bar) pourrait être compilé en un
code équivalent. Par exemple:
? (PP (COMPILER-FILTRER3 '(FOO ?- BAR)))(LAMBDA (EXPRESSION)
(AND (PAIR? EXPRESSION)
(EQUAL? (CAR EXPRESSION) 'FOO)
(AND (PAIR? (CDR EXPRESSION))
#t
(AND (PAIR? (CDR (CDR EXPRESSION)))
(EQUAL? (CAR (CDR (CDR EXPRESSION))) 'BAR)
(EQUAL? (CDR (CDR (CDR EXPRESSION))) '())))))
Concevoir la fonction compiler-filtrer3 réalisant cet effet.
On pourra dans un premier temps ne pas traiter le trou extensible.
Solution de l'exercice 36 : Observez que c'est un saupoudrage d'accents graves ou aigus et de virgules.
;;;
(define (compiler-filtrer3 filtre)
(define (filtrer3-liste expressions filtres)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(let ((loop (gensym))
(e (gensym)) )
`(let ,loop ((,e ,expressions))
(or ,(filtrer3-liste e (cdr filtres))
(and (pair? ,e)
(,loop (cdr ,e)) ) ) ) )
`(and (pair? ,expressions)
,(filtrer3 `(car ,expressions) (car filtres))
,(filtrer3-liste `(cdr ,expressions) (cdr filtres)) ) )
`(equal? ,expressions ',filtres) ) )
(define (filtrer3 expression filtre)
(if (equal? filtre '?-)
'#t
(if (equal? filtre '...)
`(error 'filtrer3 "... ne peut survenir ici")
(if (pair? filtre)
(filtrer3-liste expression filtre)
`(equal? ,expression ',filtre) ) ) ) )
`(lambda (expression) ,(filtrer3 'expression filtre)) )
Exercice 37 : Ajouter à la fonction filtrer3 le filtre *or qui permet
d'exprimer un choix de filtres. Par exemple:
? (FILTRER4 '(B) '((*OR A B)))
Solution de l'exercice 37 :
;;;
(define (filtrer4 expression filtre)
(define (filtrer4-liste expressions filtres)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(or (filtrer4-liste expressions (cdr filtres))
(and (pair? expressions)
(filtrer4-liste (cdr expressions) filtres) ) )
(and (pair? expressions)
(filtrer4 (car expressions) (car filtres))
(filtrer4-liste (cdr expressions) (cdr filtres)) ) )
(equal? expressions filtres) ) )
(define (filtrer4-or expression filtres)
(if (pair? filtres)
(or (filtrer4 expression (car filtres))
(filtrer4-or expression (cdr filtres)) )
#f ) )
(or (equal? filtre '?-)
(if (equal? filtre '...)
(error 'filtrer4 "... ne peut survenir ici") )
(if (pair? filtre)
(if (equal? (car filtre) '*or)
(filtrer4-or expression (cdr filtre))
(filtrer4-liste expression filtre) )
(equal? expression filtre) ) ) )
Exercice 38 : Ajouter la précédente fioriture au compilateur déjà
réalisé (compiler-filtre3). Par exemple:
? (PP (COMPILER-FILTRER4 '(... (*OR PERE MERE) ...)))(LAMBDA (EXPRESSION)
(LET g1120 ((g1119 EXPRESSION))
(OR (AND (PAIR? g1119)
(OR (EQUAL? (CAR g1119) 'PERE)
(OR (EQUAL? (CAR g1119) 'MERE) #f))
(LET g1122 ((g1121 (CDR g1119)))
(OR (EQUAL? g1121 '())
(AND (PAIR? g1121) (g1122 (CDR g1121))))))
(AND (PAIR? g1119) (g1120 (CDR g1119))))))
Solution de l'exercice 38 :
;;;
(define (compiler-filtrer4 filtre)
(define (filtrer4-liste expressions filtres)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(let ((loop (gensym))
(e (gensym)) )
`(let ,loop ((,e ,expressions))
(or ,(filtrer4-liste e (cdr filtres))
(and (pair? ,e)
(,loop (cdr ,e)) ) ) ) )
`(and (pair? ,expressions)
,(filtrer4 `(car ,expressions) (car filtres))
,(filtrer4-liste `(cdr ,expressions) (cdr filtres)) ) )
`(equal? ,expressions ',filtres) ) )
(define (filtrer4-or expression filtres)
(if (pair? filtres)
`(or ,(filtrer4 expression (car filtres))
,(filtrer4-or expression (cdr filtres)) )
'#f ) )
(define (filtrer4 expression filtre)
(if (equal? filtre '?-)
'#t
(if (equal? filtre '...)
`(error 'filtrer4 "... ne peut survenir ici")
(if (pair? filtre)
(if (equal? (car filtre) '*or)
(filtrer4-or expression (cdr filtre))
(filtrer4-liste expression filtre) )
`(equal? ,expression ',filtre) ) ) ) )
`(lambda (expression) ,(filtrer4 'expression filtre)) )
Recherche de motifs
La technique de Boyer-Moore est à la base d'algorithmes rapides de
recherche d'un mot dans une phrase. Pour chercher le mot babar,
on recherche d'abord la lettre r. Si la lettre correspondante du
texte est un r, on teste les précédentes (de la droite vers la
gauche). Si la lettre n'est pas un r mais, par exemple, un z
alors, comme z n'apparaît pas dans le mot babar on peut
se décaler dans le texte de cinq positions et recommencer.
Exercice 39 : Écrire la fonction boyer-moore qui prend un motif et un texte
et retourne le segment terminal de texte commençant par motif ou
#f si motif n'apparaît pas dans texte. Par exemple:
(boyer-moore '(b a b a r)
'(e n c o r e - g a b a r i t - b a b a r - f u t - g r a n d) )
® (b a b a r - f u t - g r a n d)
Ce calcul induit les comparaisons que montre le schéma suivant:
e n c o r e - g a b a r i t - b a b a r - f u t - g r a n d
. . . . r r Î babar
. . . o r o Ï babar, decalage de 5
. . . . r b Ï babar, decalage de 2
. . . . r
. . . a r
. . b a r
. a b a r
g a b a r g Ï babar, decalage de 5
. . . . r a Î babar, decalage de 1
. . . . r b Î babar, decalage de 2
. . . . r
Pour simplifier, le décalage à effectuer ne sera fonction que de la lettre
provoquant l'échec.
Solution de l'exercice 39 :
(define (boyer-moore motif texte)
(let ((fitom (reverse motif)))
(define (bm lettres longueur texte)
(if (pair? lettres)
(if (>= (length texte) longueur)
(let ((lettre-en-regard (list-ref texte longueur)))
(if (equal? (car lettres) lettre-en-regard)
(bm (cdr lettres) (- longueur 1) texte)
(let ((n (decalage lettre-en-regard lettres)))
(bm fitom (- (length motif) 1) (list-tail texte n)) ) ) )
#f )
texte ) )
(bm fitom (- (length motif) 1) texte) ) )
;;;;;;;;;;;;;;;;
(define (decalage lettre fitom)
(define (calcul lettre fitom resultat)
(if (and (pair? fitom)
(not (equal? lettre (car fitom))) )
(calcul lettre (cdr fitom) (+ 1 resultat))
resultat ) )
(calcul lettre fitom 0) )
Exercice 40 : Écrire une fonction prenant un motif et retournant la définition
d'une fonction qui attendra un texte et cherchera la première
occurrence du motif en lui. On s'attachera à précalculer ce que
l'on peut déduire du motif. Voici un exemple (il va de soi que l'on
peut mieux exploiter le motif):
? (PP (COMPILER-BOYER-MOORE '(B A B A R)))(LAMBDA (TEXTE)
(LET CBMF ((TEXTE TEXTE))
(IF (>= (LENGTH TEXTE) 5)
(CASE (LIST-REF TEXTE 4)
((R)
(CASE (LIST-REF TEXTE 3)
((A)
(CASE (LIST-REF TEXTE 2)
((B)
(CASE (LIST-REF TEXTE 1)
((A)
(CASE (LIST-REF TEXTE 0)
((B) TEXTE)
(ELSE (CBMF (LIST-TAIL TEXTE 5)))))
((B) (CBMF (LIST-TAIL TEXTE 2)))
(ELSE (CBMF (LIST-TAIL TEXTE 5)))))
((A) (CBMF (LIST-TAIL TEXTE 1)))
(ELSE (CBMF (LIST-TAIL TEXTE 5)))))
((B) (CBMF (LIST-TAIL TEXTE 2)))
(ELSE (CBMF (LIST-TAIL TEXTE 5)))))
((A) (CBMF (LIST-TAIL TEXTE 1)))
((B) (CBMF (LIST-TAIL TEXTE 2)))
(ELSE (CBMF (LIST-TAIL TEXTE 5))))
#f)))
Solution de l'exercice 40 :
(define (compiler-boyer-moore motif)
(define (cbm motif texte)
(let ((fitom (reverse motif)))
(define (ibm lettres texte)
(if (pair? lettres)
`(case (list-ref ,texte ,(- (length lettres) 1))
((,(car lettres))
,(ibm (cdr lettres) texte) )
,@(let enum ((lettres (cdr lettres))
(dejavues (list (car lettres))) )
(if (pair? lettres)
(if (member (car lettres) dejavues)
(enum (cdr lettres) dejavues)
`(((,(car lettres))
(cbmf (list-tail
,texte
,(decalage (car lettres) fitom))) )
,@(enum (cdr lettres)
(cons (car lettres) dejavues) ) ) )
`((else (cbmf (list-tail ,texte ,(length motif))))) ) ) )
texte ) )
`(let cbmf ((,texte ,texte))
(if (>= (length texte) ,(length motif))
,(ibm fitom texte)
#f ) ) ) )
`(lambda (texte)
,(cbm motif 'texte) ) )
De l'abréviation comme l'un des beaux-arts
Exercice 41 : Écrire une macro, nommée ifn, telle que
(ifn a b g) soit équivalente à
(if (not a) b g) (on peut faire mieux).
Dans un deuxième temps, adapter la solution afin de rendre
g optionnel ou prenant un nombre quelconque de formes.
Par exemple
? (IFN (= 1 1) 2 3)
= 3
? (IFN2 (= 1 1) 2 3 4)
= 4 ;
? (IFN2 (= 1 2) 3)
= 3
Solution de l'exercice 41 : La version suivante évite la capture éventuelle de la variable
not.
;;;
(define-macro (ifn condition alors sinon)
`(if ,condition ,sinon ,alors) )
(define-macro (ifn2 condition alors . sinon)
(if (pair? sinon)
`(if ,condition (begin . ,sinon) ,alors)
`(if (not ,condition) ,alors) ) )
Exercice 42 : Écrire une macro (yf a b g) telle que
a est tout d'abord évaluée. Si sa valeur est non fausse, ce
doit être une fonction et la valeur de la forme yf est la
valeur de cette fonction appliquée à b sinon c'est la valeur
de g. Par exemple:
? (YF CAR '(1 2) 3)
= 1
? (YF (= 1 2) '(1 2) 3)
= 3
Solution de l'exercice 42 : On fera attention aux environnements où les calculs doivent être
effectués.
(define-macro (yf condition alors sinon)
`(let ((condition ,condition)
(alors (lambda () ,alors))
(sinon (lambda () ,sinon)) )
(if condition
(condition (alors))
(sinon) ) ) )
Exercice 43 : Étudier le programme suivant (connu sous le nom d'Eliza ou doctor et
présent en de nombreux endroits, notamment sous Emacs) et dont
voici une illustration:
? (Freud)
Allongez-vous et causons.
(je me sens si fatigue actuellement)
Racontez-moi cela en detail.
(vous etes de la police ?)
Parlez-moi plutot de vous.
(c est a cause de ma mere)
Comment s'est deroule votre enfance ?
(cela n a pas de rapport)
Je ne vous comprend pas tres bien.
(vous etes stupide)
Parlez-moi plutot de vous.
(pourquoi)
Soyez plus explicite.
(pourquoi voulez vous savoir)
Je ne vous comprend pas tres bien.
(au revoir)
L'important, c'est de vouloir guerir ...
Cela vous fera 376 francs.
La fonction Freud et les comportements sont ainsi définis:
;;;
(define (Freud)
(define (repondre phrase base)
(if (pair? base)
(let ((filtre (caar base))
(reponse (cdar base)) )
(if (filtre phrase)
(reponse phrase)
(repondre phrase (cdr base)) ) )
(begin (display "Je ne vous comprend pas tres bien.")
(newline)
#t ) ) )
(define (au-revoir n)
(display "L'important, c'est de vouloir guerir ...")(newline)
(display "Cela vous fera ")
(display (* n 47))
(display " francs.") )
(display "Allongez-vous et causons.")(newline)
(let analyse ((e (read))(n 1))
(if (eof-object? e)
(au-revoir n)
(if (repondre e comportement-de-Freud)
(analyse (read) (+ 1 n))
(au-revoir n) ) ) ))
(define comportement-de-Freud '())
(define-macro (definir-comportement filtre . comportement)
`(begin
(set! comportement-de-Freud
(cons (cons ,(compiler-filtrer4 filtre)
(lambda (phrase) . ,comportement) )
comportement-de-Freud ) )
'OK ) )
(definir-comportement
(*or (au revoir) (adieu))
#f ) ;
(definir-comportement
((*or j je) ... (*or deprime fatigue) ...)
(display "Racontez-moi cela en detail.")
(newline)
#t ) ;
(definir-comportement
((*or vous tu) ...)
(display "Parlez-moi plutot de vous.")
(newline)
#t )
(definir-comportement
(?-)
(display "Soyez plus explicite.")
(newline)
#t )
(definir-comportement
(... (*or pere mere) ...)
(display "Comment s'est deroule votre enfance ?")
(newline)
#t )
On demande d'abstraire ce programme de manière à pouvoir créer
simplement des psychologues différents. On s'attachera à définir
une fonction creer-psychologue et une macro de définition de
comportements qui s'emploiera comme suit:
(define-psychologue Freud
(definir-comportement motif
réaction )
... )
Enfin on crééra, de toute pièce, un nouveau psychologue.
Solution de l'exercice 43 : On pourrait paramétrer aussi le tarif, la phrase initiale, la phrase
finale etc.
(define (creer-psychologue comportement)
(define (repondre phrase base)
(if (pair? base)
(let ((filtre (caar base))
(reponse (cdar base)) )
(if (filtre phrase)
(reponse phrase)
(repondre phrase (cdr base)) ) )
;;
#f ) )
(define (au-revoir n)
(display "Cela vous fera ")
(display (* n 47)) ;
(display " francs.") )
(lambda ()
(display "Allongez-vous et causons.")(newline)
(let analyse ((e (read))(n 1))
(if (eof-object? e)
(au-revoir n)
(if (repondre e comportement)
(analyse (read) (+ 1 n))
(au-revoir n) ) ) ) ) )
(define-macro (definir-psychologue nom . comportements)
`(define ,nom
(creer-psychologue
(list ,@comportements) ) ) )
(define-macro (definir-comportement filtre . comportement)
`(begin
(set! comportement-de-Freud
(cons (cons ,(compiler-filtrer4 filtre)
(lambda (phrase) . ,comportement) )
comportement-de-Freud ) )
'OK ) )
Et voici un psychologue rudimentaire:
(definir-psychologue Dumbkopf
(definir-comportement (... Freud ...)
(display "Sortez immediatement de mon cabinet!")
(newline)
#f )
(definir-comportement (...)
(display "Pouvez-vous repeter?")
(newline)
#t ) )
5 Flots
Au fil des flots ou comment manipuler des listes infinies.
On rappelle que les flots sont manipulés comme suit:
;;;
(define-macro (cons-stream head tail)
`(cons ,head (delay ,tail)) )
(define (head stream)
(car stream) )
(define (tail stream)
(force (cdr stream)) )
(define (make-empty-stream)
'() )
(define (empty-stream? stream)
(null? stream) )
Exercice 44 : Définir la fonction map-stream1 qui applique une fonction sur
tous les termes d'un flot.
Solution de l'exercice 44 :
;;;;;;;;;;;;;;;;
;;;
(define (map-stream1 fonction stream)
(if (empty-stream? stream)
the-empty-stream
(cons-stream (fonction (head stream))
(map-stream1 fonction (tail stream)) ) ) )
Exercice 45 : Définir le flot des entiers naturels. On pourra pour cela utiliser
la fonction précédente (map-stream) et le flot des entiers
naturels lui-même.
Solution de l'exercice 45 :
(define integers
(cons-stream 0 (map-stream (lambda (n) (+ 1 n)) integers)) )
Exercice 46 : Concevoir une fonction retournant les n premiers termes d'un flot.
Par exemple:
? (EXTRAIRE INTEGERS 10)
= (0 1 2 3 4 5 6 7 8 9)
Solution de l'exercice 46 :
(define (extraire stream n)
(if (empty-stream? stream)
the-empty-stream?
(if (> n 0)
(cons (head stream)
(extraire (tail stream) (- n 1)) )
'() ) ) )
Exercice 47 : Écrire la fonction fusionnant équitablement deux flots. Par
exemple:
? (EXTRAIRE
(FUSIONNER INTEGERS (MAP-STREAM - INTEGERS))
10)
= (0 0 1 -1 2 -2 3 -3 4 -4)
Solution de l'exercice 47 :
(define (fusionner stream1 stream2)
(if (empty-stream? stream1)
stream2
(if (empty-stream? stream2)
stream1
(cons-stream (head stream1)
(cons-stream (head stream2)
(fusionner (tail stream1)
(tail stream2) ) ) ) ) ) )
Exercice 48 : Étendre la fonction map-stream afin qu'elle puisse traiter
un, deux ou plusieurs flots. La fonction s'arrêtera dès qu'un des
flots se tarit.
Solution de l'exercice 48 :
(define (map-stream fonction . streams)
(case (length streams)
((0) the-empty-stream)
((1) (map-stream1 fonction (car streams)))
(else
(if (any? empty-stream? streams)
the-empty-stream
(cons-stream (apply fonction (map head streams))
(apply map-stream fonction (map tail streams)) ) ) ) ) )
Exercice 49 : Quels sont les premiers termes de la suite qui fusionnée avec les
entiers naturels est identique à elle-même.
Solution de l'exercice 49 :
(define self-integers
(cons-stream (head integers)
(fusionner self-integers (tail integers)) ) )
Les premiers termes sont:
? (EXTRAIRE SELF-INTEGERS 25)
= (0 0 1 0 2 1 3 0 4 2 5 1 6 3 7 0 8 4 9 2 10 5 11 1 12)
? (EXTRAIRE (FUSIONNER INTEGERS SELF-INTEGERS) 25)
= (0 0 1 0 2 1 3 0 4 2 5 1 6 3 7 0 8 4 9 2 10 5 11 1 12)
Notez que l'on ne peut écrire directement l'expression auto-référente
(define self-integers (cons-stream integers self-integers)).
Exercice 50 : Le problème dit de Hamming est d'obtenir la liste des entiers
multiples de 2, 3 ou 5 en ordre croissant. Le résoudre.
Solution de l'exercice 50 :
(define hamming
(let ((integers+ (tail integers)))
(ordonner <
(map-stream (lambda (n) (* 2 n)) integers+)
(ordonner <
(map-stream (lambda (n) (* 3 n)) integers+)
(map-stream (lambda (n) (* 5 n)) integers+) ) ) ) )
(define (ordonner predicat stream1 stream2)
;;
(if (empty-stream? stream1)
stream2
(if (empty-stream? stream2)
stream1
(cond ((predicat (head stream1) (head stream2))
(cons-stream (head stream1)
(ordonner predicat (tail stream1) stream2) ) )
((predicat (head stream2) (head stream1))
(cons-stream (head stream2)
(ordonner predicat stream1 (tail stream2)) ) )
(else (ordonner predicat stream1 (tail stream2))) ) ) ) )
Le début de ce flot est
? (EXTRAIRE HAMMING 25)
= (2 3 4 5 6 8 9 10 12 14 15 16 18 20 21 22 24 25 26 27 28 30 32 33 34)
6 Scheme en Scheme
Où lectrices et lecteurs découvriront, abasourdis,
l'interprète Scheme écrit en Scheme lui-même et ce qui s'ensuivra.
Voici la définition d'un interprète Scheme en Scheme:
(define (evaluate e env)
(if (atom? e) ;
(cond ((symbol? e) (lookup e env))
((or (number? e) (string? e) (char? e) (boolean? e))
e )
(else (wrong "Cannot evaluate" e)) )
(case (car e)
;;
((quote) (cadr e))
((if) (if (evaluate (cadr e) env)
(evaluate (caddr e) env)
(evaluate (cadddr e) env) ))
;;
((begin) (eprogn (cdr e) env))
((set!) (update! (cadr e) env (evaluate (caddr e) env)))
((lambda) (make-function (cadr e) (cddr e) env))
(else (invoke (evaluate (car e) env)
(evlis (cdr e) env) )) ) ) )
Deux itérateurs évaluant leur premier argument:
;;;
(define (evlis exps env)
(if (pair? exps)
(cons (evaluate (car exps) env)
(evlis (cdr exps) env) )
'() ) )
(define (eprogn exps env)
(if (pair? exps)
(if (pair? (cdr exps))
(begin (evaluate (car exps) env)
(eprogn (cdr exps) env) )
(evaluate (car exps) env) )
'() ) )
La représentation des fonctions:
;;;
(define (make-function variables body env)
(lambda (values)
(eprogn body (extend env variables values)) ) )
(define (invoke fn args)
(if (procedure? fn)
(fn args)
(wrong "Not a function" fn) ) )
La représentation des environnements:
;;;
;;;
(define (lookup id env)
(if (pair? env)
(if (eq? (caar env) id)
(cdar env)
(lookup id (cdr env)) )
(wrong "No such binding" id) ) )
(define (update! id env value)
(if (pair? env)
(if (eq? (caar env) id)
(set-cdr! (car env) value)
(update! id (cdr env) value) )
(wrong "No such binding" id) ) )
(define (extend env names values)
(cond ((pair? names)
(if (pair? values)
(cons (cons (car names) (car values))
(extend env (cdr names) (cdr values)) )
(wrong "Too less values") ) )
((null? names)
(if (null? values)
env
(wrong "Too much values") ) )
((symbol? names) (cons (cons names values) env)) ) )
L'environnement initial:
(define env.init '())
;;;
(define env.global env.init)
Les définisseurs de liaisons prédéfinies:
(define-macro (definitial name value)
`(begin (set! env.global (cons (cons ',name ,value) env.global))
',name ) )
(define-macro (defprimitive name value arity)
`(definitial ,name
(lambda (values)
(if (= (length values) ,arity)
(apply ,value values)
(wrong "Incorrect arity"
(list ',name values) ) ) ) ) )
(define the-false-value #f)
(define-macro (defpredicate name value arity)
`(definitial ,name
(lambda (values)
(if (= ,arity (length values))
(or (apply ,value values) the-false-value)
(wrong "Incorrect arity"
(list ',name values) ) ) ) ) )
Quelques fonctions prédéfinies:
(defprimitive car car 1)
(defprimitive cons cons 2)
Lancement de l'interprète:
;;;
(define (toplevel)
(display (evaluate (read) env.global))
(toplevel) )
Exercice 51 : Modifier le lancement de l'interprète pour ajouter une bannière,
une invite et détecter la fin de fichier.
Solution de l'exercice 51 :
(define (scheme)
(display "Bienvenue !")
(newline)
(let toplevel ()
(display "?? ")
(let ((e (read)))
(if (eof-object? e)
(begin (display ";;;
(newline) )
(let ((r (evaluate e env.global)))
(display "== ")
(display r)
(newline)
(toplevel) ) ) ) ) )
Exercice 52 : Définir les fonctions list et apply pour cet
interprète. On pourra se limitera à un apply binaire.
Solution de l'exercice 52 : Voici un apply n-aire. Comme list est aussi une fonction
n-aire, on définira auparavant un définisseur de fonctions n-aires.
(defnaryprimitive list
(lambda values values)
0 )
(define-macro (defnaryprimitive name value arity)
`(definitial ,name
(lambda (values)
(if (>= (length values) ,arity)
(apply ,value values)
(wrong "Incorrect arity"
(list ',name values) ) ) ) ) )
(defnaryprimitive apply
(lambda values
(define (listify arguments)
(if (pair? (cdr arguments))
(cons (car arguments) (listify (cdr arguments)))
(car arguments) ) )
(invoke (car values) (listify (cdr values))) )
2 )
Exercice 53 : Changer la représentation des fonctions afin que la valeur de
cons dans le Scheme interprété soit la valeur de cons dans
le Scheme sous-jacent. Réécrire alors list et apply.
Solution de l'exercice 53 :
;;;
(define (make-function variables body env)
(lambda values
(eprogn body (extend env variables values)) ) )
(define (invoke fn args)
(if (procedure? fn)
(apply fn args)
(wrong "Not a function" fn) ) )
;;;
(define-macro (defprimitive name value arity)
`(definitial ,name ,value) )
(defnaryprimitive list list 0)
(defnaryprimitive apply apply 2)
Exercice 54 : Modifier l'affectation afin qu'elle crée les variables si
inexistantes.
Solution de l'exercice 54 : Les variables sont créées ici au niveau global. Il suffira de
remplacer update! par update!!.
;;;
(define (update!! id env value)
(if (pair? env)
(if (eq? (caar env) id)
(begin (set-cdr! (car env) value)
value )
(update!! id (cdr env) value) )
(begin (set-cdr! (last-pair env.global)
(list (cons id value)) )
value ) ) )
Exercice 55 : Compte-tenu de l'interprète donné ci-avant, ajouter le code
nécessaire permettant de tracer l'évaluation des expressions qui
lui sont soumises.
Solution de l'exercice 55 : On ajoutera par exemple en tête de la fonction evaluate, la
verrue suivante:
(define (evaluate e env)
(display `(evaluation de ,e))(newline)
(let ((resultat code original))
(display `(le resultat est ,resultat))(newline)
resultat ) )
Exercice 56 : Au lieu d'imprimer bestialement, procurer à l'utilisateur la
possibilité d'indiquer les seuls appels qu'il souhaite voir (cf.
trace) ou bien lui offrir une nouvelle boucle d'interaction locale
lui permettant d'inspecter l'environnement.
Solution de l'exercice 56 : On écrira par exemple:
(define (evaluate e env)
(display `(ATTENTION je vais evaluer ,e))(newline)
(toplevel env) ;
(let* ((resultat code original)
(nom 'resultat)
(env (extend env (list nom) (list resultat))) )
(display `(ATTENTION le ,nom est ,resultat))(newline)
(toplevel env) ;
(lookup nom) ) )
Exercice 57 : Modifier l'interprète précédent pour qu'un nombre en
position fonctionnelle soit analogue à un sélecteur de liste. Un
nombre positif correspondra à cadnr tandis qu'un nombre
négatif correspondra à cd-nr. Par exemple
? (NOUVEL-EVAL '(2 '(A B C D)))
= C
? (NOUVEL-EVAL '(-2 '(A B C D)))
= (C D)
Solution de l'exercice 57 : On raffinera la fonction invoke pour accepter les nombres.
;;;
(define (invoke fn args)
(cond ((procedure? fn)
(apply fn args) )
((integer? fn)
(if (>= fn 0) (list-ref (car args) fn)
(list-tail (car args) (- fn)) ) )
(else (wrong "Cannot invoke" fn)) ) )
Exercice 58 : Modifier l'interprète précédent afin d'autoriser une écriture
infixe des fonctions. Par exemple:
? (AUTRE-EVAL '(1 + (3 * 4)))
= 13
Solution de l'exercice 58 : On raffinera encore invoke pour accepter cette syntaxe.
;;;
(define (invoke fn args)
(cond ((procedure? fn)
(apply fn args) )
((and (pair? args) (procedure? (car args)))
(invoke (car args) (cons fn (cdr args))) )
(else (wrong "Cannot invoke" fn)) ) )
Macro-expansion
Exercice 59 : Ajouter une phase de macroexpansion à l'interprète. On commencera
par écrire une fonction prenant une expression, l'arpentant et
remplaçant toute expression, dont le car est un symbole
connu, par le résultat de l'expanseur associé à ce
symbole. Ensuite on insérera ce macro-expanseur dans la boucle
d'interaction et on créera une macro prédéfinie de définition
de macros. Voici un exemple:
? (define-macro (foo x)
(list 'quote (list x x)) )
= foo
? (foo 3)
= (3 3)
Solution de l'exercice 59 : Le modèle qui suit ne permet pas de macro locales. Il ne procure
qu'un unique définisseur de macro define-macro. Celui-ci
communique avec le macro-expanseur à l'aide d'une variable
partagée. On notera l'usage d'evaluate pour convertir, à la
volée, le texte de l'expanseur en une fonction invoquable. On notera
aussi la reconnaissance de la citation pour éviter d'expanser son
paramètre.
Voici tout d'abord l'expanseur:
(define (expand-expression e)
(if (pair? e)
(case (car e)
((quote) e)
((lambda) `(lambda ,(cadr e) . ,(expand-expressions (cddr e))))
(else
(let ((expander (assoc (car e) macro-env)))
(if (pair? expander)
;;
(let ((ee (invoke (cdr expander) (list e))))
(expand ee) )
(expand-expressions e) ) ) ) )
e ) )
(define (expand-expressions e*)
(if (pair? e*)
(cons (expand-expression (car e*))
(expand-expressions (cdr e*)) )
e* ) )
(define macro-env
(list (cons 'define-macro macro-definer)) )
Voici la macro prédéfinie de création de macros. La variable
macro-env est une variable interne a l'implantation. On pourrait
aussi la rendre visible du Scheme interprété.
(define (macro-definer e)
(let* ((call (cadr e))
(body (cddr e))
(name (car call))
(vars (cdr call)) )
;;
(set! macro-env
;;
(cons (cons name (evaluate `(lambda (e)
(apply (lambda ,vars . ,body)
(cdr e) ) )
env.predefined ) )
macro-env ) )
`(quote ,name) ) )
Puis une façon d'intégrer le macro-expanseur à
la boucle d'évaluation. On utilisera une variable du Scheme
interprété pour contenir l'expanseur courant.
(define (scheme2)
(display "Bienvenue !")
(newline)
(let toplevel ()
(display "?? ")
(let ((e (expand-program (read))))
(if (eof-object? e)
(begin (display ";;;
(newline) )
(let ((r (evaluate e env.global)))
(display "== ")
(display r)
(newline)
(toplevel) ) ) ) ) )
(set! env.predefined
(cons (cons 'expand expand-expression)
;;
(append env.global '()) ) )
(define (expand-program e)
(evaluate `(expand ',e) env.predefined) )
7 Continuations
De la poursuite, interruption et reprise de calculs variés.
Échappement
Exercice 60 : Écrire une fonction prenant un arbre de nombres et retournant leur
produit. Utiliser un échappement dès qu'un des facteurs est nul.
Solution de l'exercice 60 :
;;;
(define (multiplier-arbre n*)
(call/cc
(lambda (exit)
(define (iterer n*)
(if (pair? n*)
(* (iterer (car n*))
(iterer (cdr n*)) )
(if (null? n*) 1
(if (= 0 n*)
(exit 0)
n* ) ) ) )
(iterer n*) ) ) )
Exercice 61 : Écrire une fonction prenant un symbole, une liste de symboles et
otant la première occurrence de ce premier de cette seconde. Le
partage entre le résultat et le second argument doit être
assuré. Le résultat doit être calculé en un seul balayage du
second argument.
Solution de l'exercice 61 :
(define (oter-symbole s original-s*)
(call/cc
(lambda (k)
(define (oter s*)
(if (pair? s*)
(if (eq? (car s*) s)
(cdr s*)
(cons (car s*) (oter (cdr s*))) )
(k original-s*) ) )
(oter original-s*) ) ) )
Exercice 62 : Modifier la fonction précédente de manière à ce qu'elle ôte
toutes les occurrences du symbole dans la liste de symboles. Le
partage doit toujours être maximal et le résultat acquis en un
seul balayage.
Solution de l'exercice 62 :
(define (oter-completement-symbole s s*)
(define (oter s* k)
(if (pair? s*)
(if (eq? (car s*) s)
(oter-tout (cdr s*))
(cons (car s*) (oter (cdr s*) k)) )
(k) ) )
(define (oter-tout s*)
(call/cc
(lambda (k)
(oter s* (lambda () (k s*))) ) ) )
(oter-tout s*) )
Passage de continuations
Exercice 63 : Écrire la fonction factorielle en usant de continuations explicites.
Voici un exemple de mise en oeuvre du résultat:
? (KFACT 6 (LAMBDA (X) X))
= 720
Solution de l'exercice 63 :
(define (kfact n k)
(if (> n 1)
(kfact (- n 1)
(lambda (r)
(k (* n r)) ) )
(k 1) ) )
Exercice 64 : Réécrire, en usant de continuations explicites, la fonction suivante:
(define (flatten e)
(if (pair? e)
(append (flatten (car e))
(flatten (cdr e)) )
(if (null? e) e (list e)) ) )
Solution de l'exercice 64 :
(define (kflatten e k)
(if (pair? e)
(kflatten (car e)
(lambda (ra)
(kflatten (cdr e)
(lambda (rb)
(k (append ra rb)) ) ) ) )
(if (null? e) (k e) (k (list e))) ) )
Exercice 65 : Réécrire, en usant de continuations explicites, la fonction
précédente légèrement modifiée. Prendre garde à l'ordre
des calculs.
(define (flatten2 e)
(define (flat l r)
(if (pair? l)
(flat (car l) (flat (cdr l) r))
(if (null? l) r (cons l r)) ) )
(flat e '()) )
Solution de l'exercice 65 :
(define (kflatten2 e k)
(define (kflat l r k)
(if (pair? l)
;;
(kflat (cdr l) r (lambda (result)
(kflat (car l) result k) ) )
(if (null? l) (k r) (k (cons l r))) ) )
(kflat e '() k) )
Continuations à arguments multiples
Exercice 66 : Linéariser un arbre représentant une expression arithmétique
(avec - unaire, + et - binaire). Voici quelques exemples:
? (LINEARISER '(+ (- 3) (* (- 2 3) 5)))
= (+ -- 3 * - 2 3 5)
Solution de l'exercice 66 :
(define (lineariser e)
(cond ((pair? e)
(case (car e)
((+ *)
(cons (car e) (apply append (map lineariser (cdr e)))) )
((-)
;;
(case (length (cdr e))
((1) (cons '-- (lineariser (cadr e))))
((2) (cons '- (apply append (map lineariser (cdr e))))) ) ) ) )
(else (list e)) ) )
Exercice 67 : Écrire maintenant une fonction inversant lineariser
c'est-à-dire construisant l'expression initiale à partir de sa
forme linéarisée.
Solution de l'exercice 67 :
(define (elever l)
(define (analyser l k)
(if (pair? l)
(case (car l)
((+ * -)
(analyser (cdr l)
(lambda (e1 l1)
(analyser l1
(lambda (e2 l2)
(k `(,(car l) ,e1 ,e2) l2) ) ) ) ) )
((--)
(analyser (cdr l)
(lambda (e1 l1)
(k `(- ,e1) l1) ) ) )
(else (k (car l) (cdr l))) )
(error 'elever 'termes-manquant l) ) )
(analyser l (lambda (e ll)
(if (null? ll)
e
(error 'elever 'termes-en-trop ll) ) )) )
Exercice 68 : L'identité de Bezout stipule que si n et p sont premiers entre
eux, alors il existe des nombres u et v tels que un+vp =
1. Écrire une fonction calculant ces nombres u et v et les
retournant à sa continuation. On pourra tester la fonction bezout grâce à:
(define (verifier-bezout n p)
(bezout n p (lambda (u v)
(+ (* u n) (* v p)) )) )
Solution de l'exercice 68 :
(define (bezout n p k) ;
(divide
n p (lambda (q r)
(if (= r 0)
(if (= p 1)
(k 0 1) ;
(error "not relatively prime" n p) )
(bezout
p r (lambda (u v)
(k v (- u (* v q))) ) ) ) ) ) )
Filtrage avec variables
On souhaite raffiner la fonction filtrer3 précédemment vue
à l'exercice 20 et ci-dessous rappelée, pour lui
ajouter un environnement, une A-liste permettant de mémoriser des
expressions filtrées. Voir exemples plus bas.
;;;
(define (filtrer3 expression filtre)
(define (filtrer3-liste expressions filtres)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(or (filtrer3-liste expressions (cdr filtres))
(and (pair? expressions)
(filtrer3-liste (cdr expressions) filtres) ) )
(and (pair? expressions)
(filtrer3 (car expressions) (car filtres))
(filtrer3-liste (cdr expressions) (cdr filtres)) ) )
(equal? expressions filtres) ) )
(or (equal? filtre '?-)
(if (equal? filtre '...)
(error 'filtrer3 "... ne peut survenir ici")
(if (pair? filtre)
(filtrer3-liste expression filtre)
(equal? expression filtre) ) ) ) )
Exercice 69 : Réécrire tout d'abord la fonction filtrer3 avec des
continuations. La continuation normale (de succès) représentera ce
qu'il reste à effectuer si le filtrage marche. La continuation
d'échec matérialise ce qu'il faut faire si le filtrage
échoue. La continuation d'échec ne prend pas d'argument, la
continuation de succès sera invoquée sur l'environnement (attendre
l'exercice suivant pour qu'elle prenne son utilité) et la
continuation courante d'échec. La fonction filtrer6 retournera en
fin de calcul l'environnement que l'on prendra égal à ()
(dont on rappelle qu'en Scheme r4rs, il vaut Vrai).
Solution de l'exercice 69 :
(define (filtrer6 expression filtre)
(define (filtrer6-liste expressions filtres env succes echec)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(filtrer6-liste expressions (cdr filtres) env succes
(lambda ()
(if (pair? expressions)
(filtrer6-liste (cdr expressions) filtres
env succes echec )
(echec) ) ) )
(if (pair? expressions)
(filtrer6-expression
(car expressions) (car filtres) env
(lambda (env echec)
(filtrer6-liste (cdr expressions) (cdr filtres) env
succes echec ) )
echec )
(echec) ) )
(if (equal? expressions filtres) (succes env echec) (echec)) ) )
(define (filtrer6-expression expression filtre env succes echec)
(if (equal? filtre '?-)
(succes env echec)
(if (equal? filtre '...)
(error 'filtrer6 "... ne peut survenir ici")
(if (pair? filtre)
(filtrer6-liste expression filtre env succes echec)
(if (equal? filtre expression)
(succes env echec)
(echec) ) ) ) ) )
(filtrer6-liste expression filtre '() (lambda (env echec) env) (lambda () #f)) )
Exercice 70 : Les variables seront nommées par des symboles dont le nom commence
par un point d'interrogation. Lorsqu'une variable est rencontrée la
première fois, elle est liée à la valeur qu'elle filtre et,
lorsque rencontrée les fois suivantes, elle devra être égale aux
expressions filtrées. Voici quelques exemples, le premier filtre des
listes de deux termes égaux (au sens de equal?), le second
filtre des listes de deux termes contenant une même sous-expression.
? (FILTRER7 '(A A) '(?X ?X))
= ((?X . A))
? (FILTRER7
'((A B C) (R G B))
'((... ?X ...) (... ?X ...)))
= ((?X . B))
Solution de l'exercice 70 :
(define (filtrer-variable? s)
(and (symbol? s)
(let ((str (symbol->string s)))
(and (> (string-length str) 0)
(char=? (string-ref str 0) #\?) ) ) ) )
(define (filtrer7 expression filtre)
(define (filtrer7-liste expressions filtres env succes echec)
(if (pair? filtres)
(if (equal? (car filtres) '...)
(filtrer7-liste expressions (cdr filtres) env succes
(lambda ()
(if (pair? expressions)
(filtrer7-liste (cdr expressions) filtres
env succes echec )
(echec) ) ) )
(if (pair? expressions)
(filtrer7-expression (car expressions)
(car filtres)
env
(lambda (env echec)
(filtrer7-liste (cdr expressions)
(cdr filtres)
env
succes
echec ))
echec )
(echec) ) )
(if (equal? expressions filtres) (succes env echec) (echec)) ) )
(define (filtrer7-expression expression filtre env succes echec)
(cond
((equal? filtre '?-) (succes env echec))
((equal? filtre '...) (error 'filtrer7 "... ne peut survenir ici"))
((filtrer-variable? filtre)
(let ((p (assq filtre env)))
(if (pair? p)
(if (equal? expression (cdr p))
(succes env echec)
(echec) )
(succes (cons (cons filtre expression) env) echec) ) ) )
((pair? filtre) (filtrer7-liste expression filtre env succes echec))
(else (if (equal? filtre expression)
(succes env echec)
(echec) ) ) ) )
(filtrer7-expression expression filtre '()
(lambda (env echec) env)
(lambda () #f) ) )
8 Continuations (suite)
Où l'on approche du dénouement. Bonne continuation!
Calculette
On définit le petit langage formé des expressions suivantes:
e := (+ e e) |
(- e e) |
(* e e) |
nombre |
(STO e) |
(RCL) |
(PRINT e)
Sa sémantique est celle d'une calculette avec imprimante et dotée
d'une unique mémoire. La mémoire est initialement vide et ne peut
être lue avant d'être écrite. Voici un exemple d'emploi
de cette calculette.
? (CALCULETTE1 '(* (STO 3) (PRINT (+ (RCL) 5))))===> 8
= 24
Exercice 71 : Écrire une fonction d'évaluation exécutant de telles
expressions. Analyser les continuations en jeu et leur signature.
Solution de l'exercice 71 : On pourrait bien sûr faire de la mémoire une variable locale
lue par RCL et affectée par STO. Nous emploierons toutefois des
continuations.
;;;
(define (calculette1 e)
(define (execute e s k)
(cond
((number? e) (k e s))
((pair? e)
(case (car e)
((+) (execute (cadr e) s
(lambda (r1 s1)
(execute (caddr e) s1
(lambda (r2 s2)
(k (+ r1 r2) s2) ) ) ) ))
((-) (execute (cadr e) s
(lambda (r1 s1)
(execute (caddr e) s1
(lambda (r2 s2)
(k (- r1 r2) s2) ) ) ) ))
((*) (execute (cadr e) s
(lambda (r1 s1)
(execute (caddr e) s1
(lambda (r2 s2)
(k (* r1 r2) s2) ) ) ) ))
((STO) (execute (cadr e) s
(lambda (r ss)
(k r r) ) ))
((RCL) (if s (k s s) (error 'calculette "Memoire non initialisee")))
((PRINT) (execute (cadr e) s
(lambda (r ss)
(display "===> ")(display r)(newline)
(k r ss) ) )) ) ) ) )
(execute e #f (lambda (r s) r)) )
Exercice 72 : On ajoute à la grammaire précédente l'expression (EITHER
e e) qui permet de continuer les calculs en cours soit avec la
valeur du premier argument, soit avec la valeur du second argument. La
mémoire n'est pas partagée bien qu'initialement la même et peut
évoluer au gré de chacun de ces deux calculs. Par exemple,
? (CALCULETTE2
'(PRINT (* (STO (EITHER 3 5)) (EITHER (RCL) 11))))===> 9
===> 33
===> 25
===> 55
= 55
Solution de l'exercice 72 :
(define (calculette2 e)
(define (execute e s k)
(cond
((number? e) (k e s))
((pair? e)
(case (car e)
((+) (execute (cadr e) s
(lambda (r1 s1)
(execute (caddr e) s1
(lambda (r2 s2)
(k (+ r1 r2) s2) ) ) ) ))
((-) (execute (cadr e) s
(lambda (r1 s1)
(execute (caddr e) s1
(lambda (r2 s2)
(k (- r1 r2) s2) ) ) ) ))
((*) (execute (cadr e) s
(lambda (r1 s1)
(execute (caddr e) s1
(lambda (r2 s2)
(k (* r1 r2) s2) ) ) ) ))
((STO) (execute (cadr e) s
(lambda (r ss)
(k r r) ) ))
((RCL) (if s (k s s) (error 'calculette "Memoire non initialisee")))
((EITHER) (execute (cadr e) s k)
(execute (caddr e) s k) )
((PRINT) (execute (cadr e) s
(lambda (r ss)
(display "===> ")(display r)(newline)
(k r ss) ) )) ) ) ) )
(execute e #f (lambda (r s) r)) )
Exercice 73 : On aimerait maintenant que les calculs ``parallèles'' introduits par
either soient menés de façon entrelacée. C'est ce
qu'illustre la trace suivante où l'on a tracé les expressions
calculées et leur résultat.
? (CALCULETTE3
'(PRINT (* (STO (EITHER 3 5)) (EITHER (RCL) 11))))<<< (PRINT (* (STO (EITHER 3 5)) (EITHER (RCL) 11)))
<<< (* (STO (EITHER 3 5)) (EITHER (RCL) 11))
<<< (STO (EITHER 3 5))
<<< (EITHER 3 5)
<<< 3
<<< 5
>>> 3[memory= #f]
>>> 5[memory= #f]
>>> 3[memory= 3]
>>> 5[memory= 5]
<<< (EITHER (RCL) 11)
<<< (EITHER (RCL) 11)
<<< (RCL)
<<< 11
<<< (RCL)
<<< 11
>>> 3[memory= 3]
>>> 11[memory= 3]
>>> 5[memory= 5]
>>> 11[memory= 5]
>>> 9[memory= 3]
===> 9
>>> 33[memory= 3]
===> 33
>>> 25[memory= 5]
===> 25
>>> 55[memory= 5]
===> 55
>>> 9[memory= 3]
= 9
Solution de l'exercice 73 :
(define (calculette3 e)
;;
(define (display-state fn args)
(cond ((eq? fn execute)
(display "<<< ")
(display (car args))
(newline) )
(else (display ">>> ")
(display (car args))
(display "[memory= ")
(display (cadr args))
(display "]")
(newline) ) ) )
;;
(define threads '())
(define (schedule! fn . args)
(set! threads (append threads (list (cons fn args))))
(if (pair? threads)
(let* ((thread (car threads))
(fn (car thread))
(args (cdr thread)) )
(set! threads (cdr threads))
(display-state fn args)
(apply fn args) )
;;
'done ) )
(define (add-to-scheduler! fn . args)
(set! threads (append threads (list (cons fn args)))) )
;;
(define (execute e s k)
(cond
((number? e) (schedule! k e s))
((pair? e)
(case (car e)
((+) (schedule! execute (cadr e) s
(lambda (r1 s1)
(schedule! execute (caddr e) s1
(lambda (r2 s2)
(schedule! k (+ r1 r2) s2) ) ) ) ))
((-) (schedule! execute (cadr e) s
(lambda (r1 s1)
(schedule! execute (caddr e) s1
(lambda (r2 s2)
(schedule! k (- r1 r2) s2) ) ) ) ))
((*) (schedule! execute (cadr e) s
(lambda (r1 s1)
(schedule! execute (caddr e) s1
(lambda (r2 s2)
(schedule! k (* r1 r2) s2) ) ) ) ))
((STO) (schedule! execute (cadr e) s
(lambda (r ss)
(schedule! k r r) ) ))
((RCL) (if s (schedule! k s s)
(error 'calculette "Memoire non initialisee") ))
((EITHER) (add-to-scheduler! execute (cadr e) s k)
(schedule! execute (caddr e) s k) )
((PRINT) (schedule! execute (cadr e) s
(lambda (r ss)
(display "===> ")(display r)(newline)
(schedule! k r ss) ) )) ) ) ) )
(schedule! execute e #f (lambda (r s) r)) )
Entrelacement non préemptif
Exercice 74 : Définir la fonction (either expression...) en Scheme
même. Cette fonction crée autant de tâches qu'elle a d'arguments,
en retournant tour à tour tous ses arguments à sa continuation. On
programmera aussi la forme (suicide) qui fait disparaître la
tâche courante. Le calcul entier usant des formes either ou
suicide sera supposé enveloppé par la macro with-parallelism qui retournera la liste des résultats produits. C'est
ce que montrent les exemples suivants:
? (WITH-PARALLELISM (+ 1 (SUICIDE)))
= ()
? (WITH-PARALLELISM
(LET ()
(DEFINE (IOTA START STOP)
(IF (< START STOP)
(CONS START (IOTA (+ START 1) STOP))
'()))
(DEFINE (//IOTA START STOP)
(APPLY EITHER (IOTA START STOP)))
(LIST (//IOTA 0 9))))
= ((8) (7) (6) (5) (4) (3) (2) (1) (0))
Solution de l'exercice 74 :
(define-macro (with-parallelism . body)
(let ((add-to-scheduler! (gensym))
(call-scheduler (gensym))
(threads (gensym))
(results (gensym))
(result (gensym))
(return (gensym)) )
`(call/cc
(lambda (,return)
(letrec ((either (lambda args
(call/cc (lambda (k)
(for-each (lambda (arg)
(,add-to-scheduler! k arg) )
args )
(,call-scheduler) )) ))
;;
(suicide (lambda ()
(,call-scheduler) ))
(,results '())
(,threads '())
(,call-scheduler (lambda ()
(if (pair? ,threads)
(let ((thread (car ,threads)))
(set! ,threads (cdr ,threads))
(apply (car thread) (cdr thread)) )
(,return ,results) ) ))
(,add-to-scheduler!
(lambda (f . args)
(set! ,threads (append ,threads
(list (cons f args)) )) )) )
;;
(,add-to-scheduler!
(lambda ()
(let ((,result (begin . ,body)))
(set! ,results (cons ,result ,results))
(,call-scheduler) )
(suicide) ) )
(,call-scheduler) ) ) ) ) )
Exercice 75 : Plutôt que either soit une fonction, on préfererait la
remplacer par une macro parallel. On introduira aussi une
fonction (yield) qui permet de suspendre la tâche en cours et
de redonner la main à l'ordonnanceur. Ceci permet d'introduire plus
d'asynchronisme entre tâches comme le montre l'exemple suivant:
? (WITH-PARALLELISM2
(LET ()
(DEFINE (WALK TREE)
(IF (PAIR? TREE)
(PARALLEL (WALK (CAR TREE)) (WALK (CDR TREE)))
(BEGIN (YIELD) (LIST TREE))))
(PARALLEL
(WALK '(A (B . C) ((D E) . F) . G))
(WALK '(((1 . 2) 3 (4 5) . 6) 7 8)))))
= ((()) (5) (()) (E) (4) (D) (6) (F) (()) (8) (3) (2) (1) (G) (C) (B) (7) (A))
Noter que si parallel avait été remplacé par either,
le parcours des arbres n'aurait pas été parallélisé. Voici
d'ailleurs une version révisée de //iota:
? (WITH-PARALLELISM2
(LET ()
(DEFINE (//IOTA START STOP)
(IF (< START STOP)
(PARALLEL START (//IOTA (+ START 1) STOP))
(SUICIDE)))
(LIST (//IOTA 0 9))))
= ((8) (7) (6) (5) (4) (3) (2) (1) (0))
Solution de l'exercice 75 :
(define-macro (with-parallelism2 . body)
(let ((add-to-scheduler! (gensym))
(call-scheduler (gensym))
(threads (gensym))
(results (gensym))
(result (gensym))
(return (gensym)) )
`(call/cc
(lambda (,return)
(letrec ((do-parallel
(lambda tasks
(call/cc
(lambda (k)
(map (lambda (task)
(,add-to-scheduler! task k) )
tasks )
(,call-scheduler) ) ) ) )
(suicide (lambda ()
(,call-scheduler) ))
(yield (lambda ()
(call/cc (lambda (k)
(,add-to-scheduler! k 'continue)
(,call-scheduler) )) ))
(,results '())
(,threads '())
(,call-scheduler (lambda ()
(if (pair? ,threads)
(let ((thread (car ,threads)))
(set! ,threads (cdr ,threads))
(apply (car thread) (cdr thread)) )
(,return ,results) ) ))
(,add-to-scheduler!
(lambda (f . args)
(set! ,threads (append ,threads
(list (cons f args)) )) )) )
(,add-to-scheduler!
(lambda ()
(let ((,result (begin . ,body)))
(set! ,results (cons ,result ,results))
(,call-scheduler) ) ) )
(,call-scheduler) ) ) ) ) )
Coroutines
Exercice 76 : Définir un système de coroutines. La forme (coroutine x
form...) crée une coroutine dont le point de contrôle
est supposé se trouver avant la première forme de son corps. La
fonction coroutine-resume ne peut être employée que depuis
le corps de la coroutine; elle prend une coroutine et une valeur, lie
cette dernière à la variable x, puis évalue le corps de la
coroutine à partir de son point de contrôle. La fonction coroutine-return ne peut, elle aussi, être employée que dans le
corps de la coroutine; elle prend un argument et le retourne comme
valeur à l'invoqueur de la coroutine. Lorsque les fonctions coroutine-resume ou coroutine-return sont invoquées, elles
mettent à jour le point de contrôle de la coroutine. Lorsqu'une
coroutine a invoqué coroutine-return, elle est considérée
comme épuisée et se comporte comme l'identité. Comme il faut
pouvoir lancer une coroutine en dehors de son corps, on crééra la
fonction coroutine-start pour ce faire. Voici un exemple
d'emploi:
? (LETREC ((C1 (COROUTINE
X
(DISPLAY X)
(DISPLAY (COROUTINE-RESUME C2 2))
(COROUTINE-RETURN 4)))
(C2 (COROUTINE
Y
(DISPLAY Y)
(DISPLAY (COROUTINE-RESUME C1 3))
(DISPLAY (COROUTINE-RESUME C1 5))
6)))
(COROUTINE-START C1 1))123
= 4
Solution de l'exercice 76 :
(define (coroutine-start c v)
(c v) )
(define-macro (coroutine variable . body)
(let ((value (gensym))
(return (gensym))
(behavior (gensym))
(self (gensym)) )
`(letrec ((,variable 'wait)
(,self (lambda (,value)
(set! ,variable ,value)
(coroutine-return (begin . ,body)) ))
(coroutine-resume
(lambda (c v)
(call/cc (lambda (k)
(set! ,self k)
(set! ,variable (c v))
(,self ,variable) ) )) )
(coroutine-return
(lambda (v)
(set! ,self (lambda (x) x))
v ) ) )
(lambda (x) (,self x)) ) ) )
Exercice 77 : À l'aide du système de coroutines précédent, écrire un
comparateur de frondaisons d'arbre. Ce prédicat retournera Vrai si
deux arbres ont les mêmes feuilles dans le même ordre. On ne
tiendra pas compte des listes vides. Ainsi:
? (SAME-FRINGE '(A B C) '((A . B) . C))(COMPARE A A)(COMPARE B B)(COMPARE C C)(COMPARE () (SENTINEL))
= #F
Solution de l'exercice 77 :
(define (same-fringe tree1 tree2)
(define (visit tree fn)
(define (walk tree)
(if (pair? tree)
(begin (walk (car tree))
(walk (cdr tree)) )
(if tree (fn tree)) ) )
(walk tree) )
(call/cc
(lambda (exit)
(letrec ((sentinel (list 'sentinel))
(c1 (coroutine void
(visit tree1 (lambda (leaf)
(coroutine-resume cmp leaf) ))
(coroutine-resume cmp sentinel) ))
(c2 (coroutine void
(visit tree2 (lambda (leaf)
(coroutine-resume cmp leaf) ))
(coroutine-resume cmp sentinel) ))
(cmp (coroutine leaf
(let find ((leaf1 (coroutine-resume c1 sentinel))
(leaf2 (coroutine-resume c2 sentinel)) )
(display (list 'compare leaf1 leaf2))
(if (eq? leaf1 leaf2)
(if (eq? leaf1 sentinel)
(exit #t)
(find (coroutine-resume c1 sentinel)
(coroutine-resume c2 sentinel) ) )
(exit #f) ) ) )) )
(coroutine-start cmp 'go) ) ) ) )
Entrelacement préemptif
Voici un interprète Scheme écrit avec des continuations. Tout
d'abord l'évaluateur et ses formes spéciales.
(define (evaluate e r k)
(if (atom? e)
(cond ((symbol? e) (k (lookup e r)))
(else (k e)) )
(let ((special (assq (car e) *specials*)))
(if (pair? special)
((cdr special) e r k)
(evaluate-application (car e) (cdr e) r k) ) ) ) )
(define *specials* '())
(define-macro (define-special call . body)
(let ((e (gensym)))
`(begin
(set! *specials*
(cons (cons ',(caar call)
(lambda (,e . ,(cdr call))
(apply (lambda ,(cdar call)
. ,body )
(cdr ,e) ) ) )
*specials* ) )
',(caar call) ) ) )
(define-special ((quote expression) r k)
(k expression) )
(define-special ((if condition consequent . alternant) r k)
(evaluate condition
r
(lambda (bool)
(if bool
(evaluate consequent r k)
(if (pair? alternant)
(evaluate (car alternant) r k)
(k nothing-particular) ) ) ) ) )
(define-special ((begin . forms) r k)
(evaluate-begin forms r k) )
(define-special ((set! variable form) r k)
(evaluate form
r
(lambda (v)
(k (update! variable r v)) ) ) )
(define-special ((lambda variables . body) r k)
(k (make-function variables body r)) )
(define (evaluate-application function arguments r k)
(evaluate function
r
(lambda (f)
(evaluate-arguments arguments
r
(lambda (v*)
(f k v*) ) ) ) ) )
Les itérateurs classiques:
(define (evaluate-begin forms r k)
(if (pair? forms)
(evaluate (car forms)
r
(if (pair? (cdr forms))
(lambda (v)
(evaluate-begin (cdr forms) r k) )
k ) )
(k nothing-particular) ) )
(define (evaluate-arguments arguments r k)
(if (pair? arguments)
(evaluate (car arguments)
r
(lambda (v)
(evaluate-arguments (cdr arguments)
r
(lambda (v*)
(k (cons v v*)) ) ) ) )
(k '()) ) )
La représentation des fonctions:
;;;
(define (make-function variables body r)
(lambda (k arguments)
(evaluate-begin body (extend r variables arguments) k) ) )
La représentation des environnements:
;;;
(define (lookup variable r)
(let ((binding (assq variable r)))
(if (pair? binding)
(cdr binding)
(wrong "No such binding" variable r) ) ) )
(define (update! variable r value)
(let ((binding (assq variable r)))
(if (pair? binding)
(let ((old (cdr binding)))
(set-cdr! binding value)
(if (eq? old uninitialized) value old) )
(wrong "No such binding" variable r value) ) ) )
(define (extend r variables values)
(cond
((pair? variables)
(if (pair? values)
(cons (cons (car variables) (car values))
(extend r (cdr variables) (cdr values)) )
(wrong "Missing argument" variables values) ) )
((null? variables)
(if (pair? values)
(wrong "Too much argument" values)
r ) )
((symbol? variables)
(cons (cons variables values) r) )
(else (wrong "Incorrect variable" variables)) ) )
;;;
(define r.init '())
Les définisseurs des variables globales de l'environnement initial:
(define-macro (definitial name . value)
`(begin (set! r.init
(cons (cons ',name
,(if (pair? value) (car value)
`uninitialized ) )
r.init ) )
',name ) )
(define-macro (defprimitive name primitive arity)
`(definitial ,name
(lambda (k args)
(if (= (length args) ,arity)
(k (apply ,primitive args))
(wrong "Incorrect arity for" ',name args) ) ) ) )
(define-macro (defnaryprimitive name primitive arity)
`(definitial ,name
(lambda (k args)
(if (>= (length args) ,arity)
(k (apply ,primitive args))
(wrong "Incorrect arity for" ',name args) ) ) ) )
Quelques définitions:
(defprimitive cons cons 2)
(defprimitive cdr cdr 1)
(defnaryprimitive + + 1)
(defnaryprimitive list
(lambda values values)
0 )
Enfin, comment lancer cet interprète:
(define (kScheme)
(evaluate (read) r.init display)
(kScheme) )
Exercice 78 : Définir la fonction apply dans cet interprète.
Solution de l'exercice 78 :
(definitial apply
(lambda (k values)
(define (listify arguments)
(if (pair? (cdr arguments))
(cons (car arguments) (listify (cdr arguments)))
(car arguments) ) )
(if (>= (length values) 2)
((car values) k (listify (cdr values)))
(wrong "Incorrect arity" 'apply) ) ) )
Exercice 79 : Définir la fonction call/cc dans cet interprète.
Solution de l'exercice 79 :
(definitial call/cc
(lambda (k args)
(if (= (length args) 1)
(let ((f (car args))
(kf (lambda (kk v*)
(if (= (length v*) 1)
(k (car v*))
(wrong "Incorrect arity for a continuation") ) )) )
(f k (list kf)) )
(wrong "Incorrect arity for" 'call/cc) ) ) )
Exercice 80 : Modifier l'évaluateur précédent de façon à identifier les
pas atomiques de calculs et à entrelacer ceux-ci afin de simuler un
pseudo-parallélisme.
Solution de l'exercice 80 : On définit d'abord un petit ordonnanceur:
;;;
(define (start-scheduler thunk)
(add-to-scheduler! thunk)
(call/cc (lambda (return)
(set! *return* return)
(call-scheduler!) )) )
(define *return* (lambda (x) x))
(define (add-to-scheduler! f . args)
(set! *threads* (append *threads* (list (cons f args)))) )
(define (call-scheduler!)
(if (pair? *threads*)
(let ((thread (car *threads*)))
(set! *threads* (cdr *threads*))
(apply (car thread) (cdr thread)) )
(*return* "No more threads to run") ) )
(define *threads* '())
Et on s'arrange pour que les appels à evaluate passent par
l'ordonnanceur.
;;;
(define (evaluate e r k)
(if (atom? e)
(cond ((symbol? e) (add-to-scheduler! k (lookup e r)))
(else (add-to-scheduler! k e)) )
(let ((special (assq (car e) *specials*)))
(if (pair? special)
(add-to-scheduler! (cdr special) e r k)
(add-to-scheduler! evaluate-application (car e) (cdr e) r k) ) ) )
(call-scheduler!) )
Exercice 81 : Ajouter à l'interprète précédent la forme parallel et la
fonction suicide. Voici un exemple d'emploi (noter le letrec
fait à la main puisque l'interprète n'a pas encore de macros):
? (KSCHEME1
'((LAMBDA (WALK)
(SET! WALK
(LAMBDA (TREE)
(IF (PAIR? TREE)
(PARALLEL (WALK (CAR TREE)) (WALK (CDR TREE)))
(IF (NULL? TREE) (SUICIDE) TREE))))
(PARALLEL
(WALK '(A (B . C) ((D E) . F) . G))
(WALK '(((1 . 2) 3 (4 5) . 6) 7 8))))
'WALK))kScheme= A
kScheme= 7
kScheme= B
kScheme= C
kScheme= G
kScheme= 1
kScheme= 2
kScheme= 3
kScheme= 8
kScheme= F
kScheme= 6
kScheme= D
kScheme= 4
kScheme= E
kScheme= 5
= "No more threads to run"
Solution de l'exercice 81 :
(defprimitive suicide
(lambda ()
(call-scheduler!) )
0 )
(define-special ((parallel . forms) r k)
(for-each (lambda (form)
(add-to-scheduler! evaluate form r k) )
forms )
(call-scheduler!) )
Exercice 82 : Ajouter à l'interprète précédent la forme future et la
fonction touch. Voici un exemple:
? (KSCHEME1
'((LAMBDA (FIB)
(SET! FIB
(LAMBDA (N)
(IF (< N 2)
N
((LAMBDA (FIBN-1 FIBN-2)
(+ (TOUCH FIBN-2) (TOUCH FIBN-1)))
(FUTURE (FIB (- N 1)))
(FUTURE (FIB (- N 2)))))))
(FIB 10))
'FIB))kScheme= 55
= "No more threads to run"
Solution de l'exercice 82 :
(define-special ((future form) r k)
(let ((box (list '*future* 'wait '())))
;;
(set-car! (cdr box) box)
(add-to-scheduler! evaluate
form
r
(lambda (v)
(set-car! (cdr box) v)
(for-each (lambda (task)
(add-to-scheduler! task v) )
(caddr box) )
(call-scheduler!) ) )
(add-to-scheduler! k box)
(call-scheduler!) ) )
(definitial touch
(lambda (k args)
(if (= 1 (length args))
(let ((box (car args)))
(if (and (pair? box) (eq? '*future* (car box)))
(begin
(if (eq? box (cadr box))
(set-car! (cddr box) (cons k (caddr box)))
(add-to-scheduler! k (cadr box)) )
(call-scheduler!) )
(wrong "Not a future" box) ) )
(wrong "Incorrect arity for" 'touch) ) ) )
Exercice 83 : Ajouter des canaux de communication à l'interprète. On introduira
les fonctions suivantes:
channel-create pour les créer, channel-send pour envoyer une valeur sur un canal et channel-receive pour lire une valeur dans un canal. Si une telle
valeur n'est pas présente, la tâche invocatrice est mise en
attente. Ces canaux sont assimilables à des tampons non bornés.
Solution de l'exercice 83 :
;;;
(defprimitive channel-create
(lambda ()
(vector '*channel* '() '()) )
0 )
(defprimitive channel-send
(lambda (c v)
(if (Channel? c)
(if (pair? (Channel-pending c))
(let ((k (car (Channel-pending c))))
(set-Channel-pending! c (cdr (Channel-pending c)))
(add-to-scheduler! k v) )
(begin
(set-Channel-values! c (append (Channel-values c) (list v)))
nothing-particular ) )
(wrong "Not a channel" c) ) )
2 )
(definitial channel-receive
(lambda (k args)
(if (= 1 (length args))
(let ((c (car args)))
(if (Channel? c)
(begin
(if (pair? (Channel-values c))
(let ((v (car (Channel-values c))))
(set-Channel-values! c (cdr (Channel-values c)))
(add-to-scheduler! k v) )
(set-Channel-pending!
c (append (Channel-pending c) (list k)) ) )
(call-scheduler!) )
(wrong "Not a channel" c) ) )
(wrong "Incorrect arity for" 'channel-receive) ) ) )
Exercice 84 : Ajouter à l'interprète la nouvelle forme qlambda qui assure
que son corps est évalué en exclusion mutuelle: aucune autre
invocation parallèle à la même fonction n'est possible.
Solution de l'exercice 84 : Cette forme pose un problème du fait des retours multiples dûs aux
continuations employées plusieurs fois.
(define-special ((qlambda variables . body) r k)
(k (make-qlambda-function variables body r)) )
(define (make-qlambda-function variables body r)
(let ((active? #f)
(queue '()) )
(lambda (k arguments)
(if active?
(set! queue (append queue (list (cons k arguments))))
(let enter ((k k) (arguments arguments))
(set! active? #t)
(add-to-scheduler! evaluate-begin
body
(extend r variables arguments)
(let ((exited? #f))
(lambda (v)
(if (not exited?)
(if (pair? queue)
(let ((k+args (car queue)))
(set! queue (cdr queue))
(add-to-scheduler!
enter (car k+args)
(cdr k+args) ) )
(set! active? #f) ) )
(set! exited? #t)
(k v) ) ) ) ) )
(call-scheduler!) ) ) )
9 Graphique
Ces exercices sont à faire avec DrScheme
Les images sont des rectangles dont les points sont repérés par une
abscisse et une ordonnée variant entre -1 et 1. Par défaut les carrés
créés par line et filled-triangle font 100 pixels de
côté (la valeur de la variable default-image-size.
Rappel des primitives graphiques de DrScheme:
- (line x0 y0 x1 y1)
rend une image carrée blanche avec une ligne noire tracée de (x0,y0)
vers (x1,y1).
- (quarter-turn-right image) rend une nouvelle image
tournée de 90 degrés (dans le sens des aiguilles d'une montre).
- (mirror-image image) rend une nouvelle image mémoire
reflétée (par rapport à l'axe des ordonnées).
- (invert image) rend une nouvelle image dont les
couleurs des pixels sont inversées.
- (overlay image image) superpose deux images, les pixels
blancs devenant transparents.
- (resize-image image sizex sizey) rend une nouvelle image
homothétique avec les nouvelles tailles indiquées.
- (stack image1 image2) rend une image correspondant aux
deux images collées verticalement.
- (filled-triangle x0 y0 x1 y1 x2 y2) créé une image
blanche avec un triangle noir défini par les coordonnées des trois points.
Exercice 85 : Construire une image ayant une forme de croix latine.

Solution de l'exercice 85 :
(define croix
(let* ((inf (filled-triangle -1 -1/3 -1 1/3 1 -1/3))
(sup (filled-triangle -1 +1/3 +1 1/3 1 -1/3))
(barreh (overlay inf sup))
(barrev (quarter-turn-right barreh)) )
(overlay barreh barrev) ) )
Exercice 86 : Écrire une fonction coller prenant une liste d'images et les
collant ensemble horizontalement. Par exemple: (coller (list
croix croix)) conduit à:

Solution de l'exercice 86 :
(define (coller images)
(define (colle images)
(if (pair? images)
(if (pair? (cdr images))
(stack (car images)
(colle (cdr images)) )
(car images) )
(error 'coller "pas d'image" images) ) )
(quarter-turn-right (colle images)) )
Exercice 87 : Écrire une fonction hachures creant une image remplie de 2n+1
hachures diagonales comme par exemple (hachures 4):

Solution de l'exercice 87 :
;;;
(define (hachures n)
(let ((delta (/ 2 (+ n 1))))
(let hachurer ((image (line -1 1 1 -1))
(i 1) )
(if (> i n)
(let ((complement (quarter-turn-right
(quarter-turn-right image) )))
(overlay complement image) )
(hachurer (overlay image (line -1 (- 1 (* i delta))
(- 1 (* i delta)) -1 ))
(+ i 1) ) ) ) ) )
Ce document a été traduit de LATEX par
HEVEA.



