Premiers pas en Scheme

1 Premiers pas en Scheme

Où l'on découvrira la récursion simple, double ou enveloppée ainsi que la définition de fonctions locales tout en manipulant des listes plates, des arbres binaires et même des petits entiers.

Toutes les fonctions, solutions des énoncés suivants, sont définissables en moins de 10 lignes.

Exercice 1 : Écrire la factorielle.

Solution de l'exercice 1 :

;;; A tout seigneur, tout honneur:
(define (factorielle nombre)
  (if (= nombre 1)
      1
      (* nombre (factorielle (- nombre 1))) ) )

Attention il n'y a pas de grand nombre en Scheme->C, aussi mélange-t-il flottants et entiers. En Bigloo par contre, les petits entiers sont tronqués de la même manière qu'en C. En DrScheme, les grands nombres (ou bignum en jargon) et les rationnels sont disponibles.

? (FACTORIELLE 12)
= 479001600
? (FACTORIELLE 13)
= -215430144

Exercice 2 : Écrire une fonction retournant la somme des n premiers carrés. Par exemple:

? (SOMME-CARRES 5)
= 55

Solution de l'exercice 2 : Songez à bien présenter vos programmes!

;;; Du numerique enfin !
(define (somme-carres n)
  (if (= n 0)
      0
      (+ (* n n) (somme-carres (- n 1))) ) )

Exercice 3 : Concevoir la fonction compter qui prend un symbole-lettre et une liste de symboles-lettres et compte les occurrences de ce premier parmi ces derniers. Par exemple, si poeme-pi vaut (Q U E J A I M E A F A I R E A P P R E N D R E U N N O M B R E U T I L E A U S A G E), alors:

? (COMPTER 'N POEME-PI)
= 3

Solution de l'exercice 3 :

;;; compter au premier niveau.
(define (compter mot phrase)
  (if (pair? phrase)
      (+ (if (equal? mot (car phrase)) 1 0) ; Notez l'alternative sous l'addition!
         (compter mot (cdr phrase)) )
      0 ) )

Exercice 4 : Concevoir la fonction decompter qui prend un symbole et une expression et décompte toutes les occurrences de ce premier dans cette dernière (quelque soit la profondeur de ces occurrences). Par exemple:

? (DECOMPTER 'A '((A B) ((C A)) A))
= 3
? (DECOMPTER 'C '((A B) ((C A)) A))
= 1

Solution de l'exercice 4 : La programmation suivante use de Sexpressions vues comme des arbres binaires. Ainsi ((a b) ((c a)) a) est vue comme:

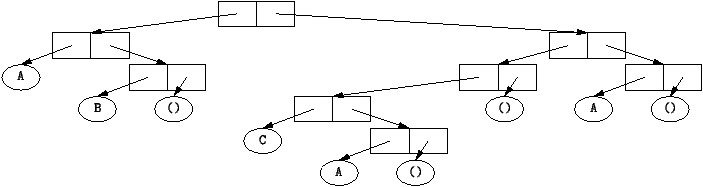
Voici la fonction:

;;; compter a tous les niveaux.
(define (decompter feuille arbre)
  (if (pair? arbre)
      (+ (decompter feuille (car arbre))   ; récursion à gauche
         (decompter feuille (cdr arbre)) ) ; récursion à droite
      (if (equal? feuille arbre)
          1
          0 ) ) )

Exercice 5 : Écrire la fonction begaie prenant une liste de symboles en argument, une phrase, et retournant en sortie une phrase où tous les mots sont répétés. Par exemple:

? (BEGAIE '(COMMENT ALLEZ VOUS))
= (COMMENT COMMENT ALLEZ ALLEZ VOUS VOUS)

Solution de l'exercice 5 :

(define (begaie phrase)
  (if (pair? phrase)                    ; si la phrase a au moins un mot
      (cons (car phrase)                ; le répéter une fois
            (cons (car phrase)          ; le répéter deux fois !
                  (begaie (cdr phrase)) ) )
      '() ) )

Exercice 6 : Écrire une fonction debegaie qui ôte d'une phrase tout bégaiement et notamment celui produit par la fonction de l'exercice précédent. Par exemple

? (DEBEGAIE (BEGAIE '(COMMENT ALLEZ VOUS)))
= (COMMENT ALLEZ VOUS)

Solution de l'exercice 6 :

(define (debegaie phrase)
  (if (pair? phrase)
      (if (pair? (cdr phrase))
          (if (equal? (car phrase)      ; si le premier mot
                      (cadr phrase) )   ; est égal au second
              (debegaie (cdr phrase))
              (cons (car phrase) (debegaie (cdr phrase))) )
          phrase )
      phrase ) )

Notez que l'on ne saurait prendre le car ou le cdr d'un objet que si l'on sait qu'il répond vrai à pair?. On ne peut donc comparer le car et le cadr que si la liste contient au moins deux termes.

Exercice 7 : Écrire la fonction impairs qui prend une liste de symboles en argument et retourne la liste de tous les symboles de rang impair. Par exemple:

? (IMPAIRS '(UN DEUX TROIS QUATRE))
= (UN TROIS)
? (IMPAIRS '(1 2 3 4 5))
= (1 3 5)

Solution de l'exercice 7 : Notez la récursion mutuelle entrecroisée:

;;; impairs est une vraie inverse de begaie.
(define (impairs liste)
  (if (pair? liste)
      (cons (car liste) (pairs (cdr liste)))
      '() ) )
(define (pairs liste)
  (if (pair? liste)
      (impairs (cdr liste))
      '() ) )

Notez que la notion de bégaiement n'est pas précise puisque des mots répétés peuvent apparaître dans une phrase normale comme (vous vous leurrez). En d'autres termes, la fonction debegaie n'est pas l'inverse de la fonction begaie tandis qu'impairs l'est. On obtiendrait ainsi:

? (IMPAIRS (BEGAIE '(VOUS VOUS LEURREZ)))
= (VOUS VOUS LEURREZ)
? (DEBEGAIE (BEGAIE '(VOUS VOUS LEURREZ)))
= (VOUS LEURREZ)

Exercice 8 : Concevoir la fonction aplatir qui prend une Sexpression en argument et retourne la liste de tous les symboles qu'elle contient dans l'ordre gauche-droite. Par exemple:

? (APLATIR '((A B) ((C))))
= (A B C)
? (APLATIR
(LIST (CONS 'A (CONS 'B 'C)) '((D B A) E)))
= (A B C D B A E)

Solution de l'exercice 8 : Là encore, on adopte la vision arbre binaire des Sexpressions.

(define (aplatir sexp)
  (if (pair? sexp)
      (append (aplatir (car sexp))    ; append coûteux ici
              (aplatir (cdr sexp)) )
      (if (symbol? sexp)
          (list sexp)
          '() ) ) )

Exercice 9 : Concevoir une fonction prenant une Sexpression et retournant une forme la calculant. Par exemple:

? (RECONSTRUIRE '(A B))
= (CONS 'A (CONS 'B '()))

Solution de l'exercice 9 : Merci à Annick Valibouze qui m'a transmis cette fonction issue du folklore lointain de P6.

;;; Piquée à Anne Valibouze, Nguyen Van Lu et d'autres. Elle
;;; s'appelait snoc alors.
(define (reconstruire exp)
  (if (pair? exp)
      (list 'cons (reconstruire (car exp))
                  (reconstruire (cdr exp)) )
      (list 'quote exp) ) )

Exercice 10 : Concevoir une fonction prenant un entier naturel en entrée et retournant la liste de ses facteurs premiers. Un algorithme simple suffira! Par exemple

? (FACTEURS-PREMIERS 625)
= (5 5 5 5)
? (FACTEURS-PREMIERS 123456)
= (2 2 2 2 2 2 3 643)

Solution de l'exercice 10 : Ceci est le premier exemple d'une sous-fonction définie localement.

;;; Premier exemple de sous-fonction locale.
(define (facteurs-premiers n)
  (define (fp n essai)
    (if (> n 1)
        (if (= 0 (remainder n essai))
            (cons essai (fp (quotient n essai) essai))
            (fp n (+ 1 essai)) )
        '() ) )
  (if (= n 1) (list 1) (fp n 2)) )

On pourrait aussi écrire '(1) à la place de (list 1).