Planche : 1
Planche : 2
Historique
Lisp 1.5: 1962 (second plus vieux langage après Fortran).
Créé par John MacCarthy au MIT.
ML: 1972, Scheme: 1975 (découvert par Steele & Sussmann, MIT).
Scheme est une reconstruction minimale de Lisp. Scheme est décrit par
un rapport (actuellement le R5RS
) de
50 pages environ.
Scheme a été normalisé par l'IEEE puis par l'ISO en 1992.
Planche : 3
Les valeurs de base
Les symboles:
Z Lisp C6H12O11 + * symbole-encore-plus-long?
La norme Scheme impose l'insensibilité à la casse.
Les nombres:
13 -813 +42
3.1415 -0.2787e+1
2/3
Les rationnels ne sont pas toujours présent, pas plus que les bignums.
Les booléens:
#t #F
#f est la seule valeur representant Faux. Toute valeur
différente de #f représente également Vrai.
Les chaînes de caractères:
"Suis-je une corde ?"
mais aussi "\"" et "\\".
Planche : 4
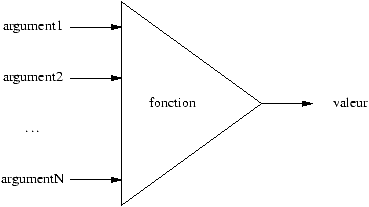
Les fonctions
Les fonctions sont des êtres prenant des arguments et retournant une
valeur.
Planche : 5
Les listes
Les listes débutent par une parenthèse ouvrante et s'achèvent par une
parenthèse fermante. Ce sont des structures ordonnées de termes de
nature quelconque.
(ceci est une liste)
(une (autre) ((liste)))
(1 un (o n e) #("Attila" 1.0000))
() ;
Planche : 6
Les programmes
Les programmes sont représentés par des listes et des symboles.
Quand on pense f(x,y), on écrit en polonaise préfixée (version dite
de Cambridge (Massachussetts)):
(f x y)
La fonction est suivie de ses paramètres.
Premiers programmes:
(- 42)
(+ 1 (* 2 3))
Les listes peuvent être hétérogènes. Il existe également les
vecteurs qui ont de meilleurs temps d'accès.
Planche : 7
Les prédicats
Ce sont des fonctions à valeur booléennes.
symbol? vector? boolean? string? null?
number? integer?
pair? procedure?
equal?
= < > >= <=
string=? char=?
Planche : 8
Manipuler des listes
(ceci est une liste) ®car ceci
(ceci est une liste) ®cdr (est une liste)
ceci
(est une liste) ®cons (ceci est une liste)
Les fonctions car et cdr attendent de leur argument qu'il soit une
liste non vide. La fonction cons attend de son second argument qu'il
soit une liste (éventuellement vide).
car, cdr sont des fonctions. Les fonctions n'altèrent pas
leurs arguments.
Planche : 9
Point d'ordre!
Trois concepts différents: nil, () et #f.
nil est un symbole comme un autre (généralement non défini
dans les systèmes Scheme).
() est la liste vide (que l'on prononce « nil »).
C'est ce que l'on obtient ainsi:
(terme) ®cdr ()
En particulier, la liste vide vaut Vrai.
#f est le booléen Faux.
En Lisp et dans les Scheme pré-r4rs, ils sont (souvent) confondus.
Planche : 10
Contrôle
Tout est parenthésé! Tout a une valeur! Rien n'est superflu!
(if condition alors sinon)
(begin faire1 faire2 ... fairen)
(quote valeur)
(define nom valeur)
(define (nom variables...) définition)
Planche : 11
Définitions
(define pi 3.1415926535)
(define moi "Je")
(define sept (+ 3 4))
(define (oppose n)
(- 0 n) ) ;
(define (abs n) ;
(if (< n 0)
(oppose n)
n ) )
(abs 3)
Planche : 12
Récursion
(mklist n 'e) ® (e e ... e)
(define (mklist n exp)
(if (> n 0)
(cons exp (mklist (- n 1) exp))
'() ) )
(mklist 2 7) ;
(if (> 2 0) (cons 7 (mklist (- 2 1) 7)) '())
(cons 7 (mklist (- 2 1) 7))
(cons 7 (mklist 1 7))
(cons 7 (if (> 1 0) (cons 7 (mklist (- 1 1) 7)) '()))
(cons 7 (cons 7 (mklist 0 7)))
(cons 7 (cons 7 (if (> 0 0) ... '())))
(cons 7 (cons 7 '()))
(cons 7 '(7))
'(7 7)
Planche : 13
Exercice: concaténation de listes
(append '(e1 e2 ... en) '(t1 t2 ... tp))
® (e1 e2 ... en t1 t2 ... tp))
Indice 1:
(append '() '(t1 t2 ... tp))
® (t1 t2 ... tp))
Indice 2:
(append '(e1 e2 ... en) '(t1 t2 ... tp))
® (e1 ...))
Solution:
(define (append l1 l2)
(if (pair? l1)
(cons (car l1) (append (cdr l1) l2))
l2 ) )
Attention à prendre la récursion à lisse-poil!
(define (append l1 l2)
(if (pair? l2)
(append (reverse (cons (car l2)
(reverse l1) ))
(cdr l2) )
l1 ) )
Planche : 14
Citation
Si les programmes sont représentés par des listes ou des symboles,
comment représenter des listes ou des symboles au sein de programmes:
comment citer des valeurs dans un programme ?
Par exemple, comment obtenir la liste (ah ah ah) ?
On ne peut écrire (mklist 3 ah)!
Il faut écrire (mklist 3 (quote ah)).
(quote (a b (c d))) ® (a b (c d))
(quote (mklist 3 (quote ah)))
® (mklist 3 (quote ah))
(mklist 3 (quote ah)) ® (ah ah ah)
Il existe une notation particulière:
'expression º (quote expression)
Planche : 15
Entrées-sorties
Impression:
(display valeur)
(newline)
Lecture:
(read)
Ce sont des fonctions génériques faisant des effets de bord.
Planche : 16
La boucle fondamentale d'interaction
(define (toplevel)
(display (eval (read)))
(toplevel) )
(define (read)
... (read-char) ... )
(define (display e)
... (write-char ...) ... )
(define (eval program ...)
... )
Planche : 17
Résumé
Des types de données disjoints: symbole, vecteur, liste, nombre,
chaîne, procédures (fonctions).
Un langage non typé mais des valeurs typées (et inspectables):
Scheme est donc un langage sûr.
Des fonctions (primitives (essentielles) ou déduites), des formes
spéciales (seulement 5 essentielles!).
Planche : 18
Terminologie
-
valeur
- Elles sont de première classe. Il n'y a aucune
restriction sur leur emploi: elles peuvent apparaître comme argument,
résultat, être stockées en liste, vecteur, variable.
- argument
- Valeur qui sera liée à une variable lors de
l'application d'une fonction.
- paramètre
- programme dont la valeur deviendra un argument.
- fonction
- ou procédure. Un prédicat est une fonction à valeur
booléenne.
- variable
- représentés par un symbole, mène à une valeur.
- forme
- un programme représenté par une liste. Ce peut être une
forme spéciale ou une application fonctionnelle
(l'application d'une fonction à ses arguments).
- forme spéciale
- une forme préfixée par un mot clé
(begin, if, quote et quelques autres)
induisant une évaluation particulière.
(define (oppose n)
((if (> n 0) + -) n) )
(oppose (oppose (+ 19 99)))
(+ 19 99) est le paramètre d'opposé.
118 est l'argument d'opposé.
n est la variable d'une fonction unaire, valeur de la
variable oppose.
La variable n a pour valeur l'argument 118.
La forme (+ 19 99) a pour valeur 118.
Pas d'ordre d'évaluation des arguments.
Ce document a été traduit de LATEX par
HEVEA.
 Rudiments de Scheme
Rudiments de Scheme