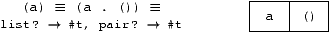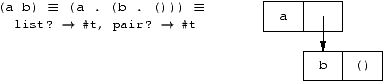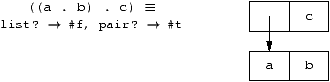Planche : 1

Le langage Scheme

Revision: 1.10

Le côté physique de Scheme

Christian Queinnec UPMC--LIP6

Planche : 2

Les paires pointées

Les listes sont représentées par des paires pointées suivant le schéma:

Rep[listeNonVide] = ( Rep[car(listeNonVide)] . Rep[cdr(listeNonVide)] )
Rep[atome] = atome

D'où le nom de paire pointée et le choix du nom pour pair?.

Est atomique tout ce qui n'est pas une liste non vide.

Planche : 3

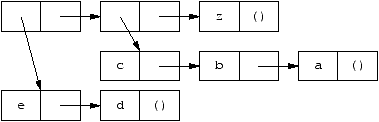
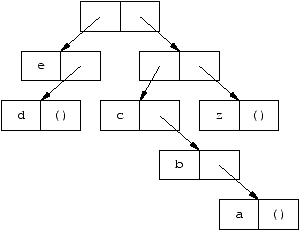
Vision liste/arbre binaire/S-expression

Soit la liste ((e d)(c b a) z):

(define (find leaf tree)
  (or (equal? leaf tree)
      (and (pair? tree)
           (or (find leaf (car tree))
               (find leaf (cdr tree)) ) ) ) )
(define (look term list)
  (if (pair? list)
      (or (if (pair? (car list))
              (look term (car list))
              (equal? term (car list)) )
          (look term (cdr list)) )
      #f ) )

Planche : 4

Modificateurs physiques

Les paires pointées sont des structures de données muables. Les « fonctions » set-car! et set-cdr! permettent de modifier les champs d'un doublet.

(let ((unePaire (cons 'a 'b)))
(set-car! unePaire 'z)
unePaire )
=> (z . b)

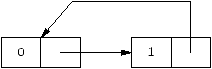
On peut donc créer des structures de données cycliques comme, par exemple, la liste infinie (0 1 0 1 0 ...):

(let ((c (list 0 1)))
(set-cdr! (cdr c) c)
c )

Attention à ne pas imprimer! En DrScheme, cela donne, comme en Common Lisp, #0=(0 1 . #0#).

Planche : 5

Égalité

Trois sortes d'égalité:

equal?: teste l'égalité structurelle de deux valeurs.
eq?: teste l'égalité physique de deux valeurs.
eqv?: teste l'égalité physique ou numérique de deux valeurs.

(equal? (cons 'a 'b) (cons 'a 'b))      ; #t
(eq? (cons 'a 'b) (cons 'a 'b))         ; #f
(let ((x (cons 'a 'b)))
  (eq? x x) )                           ; #t
(let ((x (cons 'a 'b)))
  (equal? x (begin (set-cdr! x x)
                   x )) )               ; ?

Taxonomie:

valeur	composite	terminale
muable	cons, vector, string	fermeture
immuable	symbole, "..." (possiblement)	nombre, booléen, caractère, primitive

Grands entiers alloués.

Une possible définition d'equal? (DrScheme est comme cela):

(define (equal? x y)
  (or (eq? x y)
      (cond ((pair? x)
             (and (pair? y)
                  (equal? (car x) (car y))
                  (equal? (cdr x) (cdr y)) ) )
            ((number? x)
             (and (number? y)
                  (= x y) ) )
            ...
            (else #f) ) ) )

Si (eq? x y) est vrai alors (equal? x y) ne peut être faux.

Cas (très) particulier: l'égalité des fonctions.

f = g Þ " x, f(x) = g(x)

La réciproque est connue sous le nom d'axiome d'extensionnalité en l-calcul.

(let ((f (lambda (x) (car x))))
(eq? f f) ) ; #t
(eq? car car)
(eq? cons cons)
(equal? cons cons)

Planche : 6

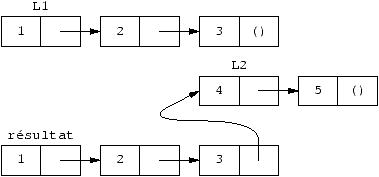
Consommation

(define (append l1 l2)
  (if (pair? l1)
      (cons (car l1)
            (append (cdr l1) l2) )
      l2 ) )

La fonction append a un coût linéaire en son premier argument.

Planche : 7

Efficacité

(iota n) ® (0 1 2 ... n-1)

(define (iota1 n)
  (if (> n 0)
      (append (iota1 (- n 1))
              (list (- n 1)) )
      '() ) )

(define (iota12 n)
  (if (> n 0)
      (append! (iota12 (- n 1))
               (list (- n 1)) )
      '() ) )
(define (append! l1 l2)
  (if (pair? l1)
      (begin
        (if (null? (cdr l1))
            (set-cdr! l1 l2)
            (append! (cdr l1) l2) )
        l1 )
      l2 ) )

(define (iota2 n)
  (define (enum beg end)
    (if (< beg end)
        (cons beg (enum (+ beg 1) end))
        '() ) )
  (enum 0 n) )

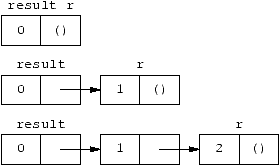
Accrochage de bord:

(define (iota3 n)
  (if (> n 0)
      (let ((result (list 0)))
        (define (add r)
          (if (< (car r) (- n 1))
              (begin
                (set-cdr! r (list (+ 1 (car r))))
                (add (cdr r)) ) ) )
        (add result)
        result )
     '() ) )

Planche : 8

Affectation

(set! variable forme)

L'affectation commence par calculer la forme puis modifie la variable en conséquence. La valeur que retourne une affectation n'est pas spécifiée.

Scheme n'est donc pas un langage purement fonctionnel de par la présence de l'affectation et de données muables.

En DrScheme, set! ne crée pas de variable globale.

L'affectation force à abandonner le modèle de calcul par substitution au profit de la notion de liaison. En effet:

(let* ((w+r (let ((shared '(hello world)))
              (cons (lambda (v)
                      (set! shared v) )
                    (lambda () shared) ) ))
       (reader (cdr w+r))
       (writer (car w+r)) )
  (reader)                ; retourne (hello world)
  (writer '(salut monde))
  (reader) )              ; retourne (salut monde)

(define (make-enumerator)
  (let ((seed 0))
    (lambda ()
       (let ((current seed))
         (set! seed (+ seed 1))
         current ) ) ) )
(define N1 (make-enumerator))
(define N2 (make-enumerator))
(list (N1) (N1) (N1) (N1) (N2)) ; (0 1 2 3 0) ou (3 2 1 0 0) ou ...

La fonction enumerator pourrait être réécrite de façon équivalente en:

(define make-enumerator
  (lambda ()
    (let ((seed 0))
      (lambda ()
         (let ((current seed))
           (set! seed (+ seed 1))
           current ) ) ) ) )

mais pas du tout comme:

(define make-enumerator
  (let ((seed 0))
    (lambda ()
      (lambda ()
         (let ((current seed))
           (set! seed (+ seed 1))
           current ) ) ) ) )

Planche : 9

La puissance de l'affectation

let était une syntaxe non primitive, letrec aussi:

(letrec ((variable₁ forme₁)
         ...
         (variable_n forme_n) )
  forme... )
                                         est équivalent à
(let ((variable₁ 'wait)
      ...
      (variable_n 'wait) )
  (set! variable₁ forme₁)
  ...
  (set! variable_n forme_n)
  forme... )

Planche : 10

Mort aux cons ou, le style par passage de message

Comment simuler des paires avec l en message-passing style ?

(define (kons a d)
  (lambda (msg)
    (case msg
      ((car) a)
      ((cdr) d)
      ((set-car!) (lambda (v) (set! a v)))
      ((set-cdr!) (lambda (v) (set! d v)))
      (else (error 'kons "incompris" msg)) ) ) )
(define (kar p)
  (p 'car) )
(define (set-kar! p v)
  ((p 'set-car!) v) )

(define unCons (kons 1 2))
(set-kar! unCons 3)
(kar unCons)                ; 3 bien sûr!

Une paire pointée est représentée par une fermeture.

Planche : 11

Promesses ou glaçons

(delay forme) ; retourne une promesse
(force promesse) ; retourne une valeur

Une implantation possible:

(delay e) º (lambda () e)
(define (force promesse)
(promesse) )

On peut améliorer delay pour ne calculer au plus qu'une fois la valeur d'une promesse.

(delay e)  º (memo (lambda () e))
(define (force promesse) (promesse))
(define (memo thunk)
  (let ((computed? #f)
        (value     'wait) )
    (lambda ()
      (if computed?
          value
          (begin (set! value (thunk))
                 (set! computed? #t)
                 value ) ) ) ) )

Planche : 12

Programmation par flots

(head flot)   rend le premier terme du flot
(tail flot)   rend un flot privé de son premier élément
(empty-stream? flot) teste si un flot est vide
(cons-stream valeur flot) crée un flot
(empty-stream)   crée le flot vide

Une première implantation:

(define head car)
(define tail cdr)
(define empty-stream? null?)
(define cons-stream cons)
(define (empty-stream) '())

Planche : 13

Somme des feuilles impaires

énumérer les feuilles => (flot de feuilles) => filtrer les feuilles => (flot d'impairs) => accumuler les résultats

(define (tree->stream tree)
  (if (pair? tree)
      (append-stream
       (tree->stream (car tree))
       (tree->stream (cdr tree)) )
      (cons-stream tree (empty-stream)) ) )

Quelques utilitaires

(define (append-stream stream1 stream2)
  (if (empty-stream? stream1)
      stream2
      (cons-stream (head stream1)
                   (append-stream (tail stream1)
                                  stream2 ) ) ) )

(define (stream-filter predicate stream)
  (if (empty-stream? stream)
      (empty-stream)
      (if (predicate (head stream))
          (cons-stream
           (head stream)
           (stream-filter predicate
                          (tail stream) ) )
          (stream-filter predicate
                         (tail stream) ) ) ) )

Accumulation:

(define (stream-reduce f end stream)
  (if (empty-stream? stream)
      end
      (f (head stream)
         (stream-reduce f end (tail stream)) ) ) )
(define (stream-nth n stream)
  (if (= n 0)
      (head stream)
      (stream-nth (- n 1) (tail stream)) ) )

Une solution (enfin):

(define (count-odd-leaves tree)
  (stream-reduce
   +
   0
   (stream-filter
    (lambda (leaf)
      (and (number? leaf) (odd? leaf)) )
    (tree->stream tree) ) ) )

Moralité: moins de récursion, plus d'itérations (à la STL).

Planche : 14

Le flot des entiers

Et si l'on écrivait:

(define (entiers start)
(cons start (entiers (+ start 1))) )

(0 1 2 3 ...)

(cadr (entiers 0))

Écrivons alors:

(define (integers start)
(cons-stream start (integers (+ start 1))) )
(head (tail (integers 0)))

(0 . #<entiers à partir de 1>)

(0 1 . #<entiers à partir de 2>)

Planche : 15

Seconde implantation

(define head car)
(define empty-stream? null?)
(define (empty-stream) '())
(define-macro (cons-stream elt s)
`(cons ,elt (delay ,s)) )
(define (tail s)
(force (cdr s)) )

Planche : 16

Quelques flots

Le flot des nombres de Fibonacci:

F_n+2 = F_n + F_n+1, F₁ = F₀ = 1

(define (generate-fibonacci fn fn+1)
  (cons-stream
   fn
   (generate-fibonacci fn+1 (+ fn fn+1)) ) )

Les entiers revisités:

(define (map-stream f stream)
  (if (empty-stream? stream)
      (empty-stream)
      (cons-stream (f (head stream))
                   (map-stream f (tail stream)) ) ) )
(define integers
  (cons-stream 0
               (map-stream (lambda (n) (+ n 1))
                           integers ) ) )

Ce document a été traduit de L^AT_EX par H^EV^EA.