Planche : 1

Le langage Scheme

Revision: 1.5

L'interprète du DEUG

Christian Queinnec UPMC--LIP6

Planche : 2

L'interprète

L'interprète est, bien sûr, sur le réseau .

Il ne sait interpréter qu'une unique expression (cela élimine les problèmes de persistence de la boucle fondamentale d'interprétation). En revanche, il peut s'auto-interpréter.

Planche : 3

Structure

(define (deug-eval e)
  utilitaires divers: cadr cdddr length map member
  expansion de cond
  types abstraits pour syntaxe: alternative? alternative-condition
  représentation d'environnements
  fonctions environnementales: lookup extend enrich
  évaluateurs spécialisés par formes spéciales: evaluate-variable
  évaluateur général: evaluate
  itérateurs d'évaluation: eprogn evlis
  représentation de fonctions: create-function invoke
  représentation des primitives: create-primitive
  syntaxe de description des primitives: describe-primitive
  création de l'environnement global initial
  (evaluate e initial-environment) )

Planche : 4

Utilitaires divers

Des compositions de car ou cdr diverses et nécessaires pour écrire les accesseurs syntaxiques pour les formes spéciales de Scheme.

Quelques utilitaires supplémentaires comme length, map, member et rank. Tous ont des schémas de récursion classiques et seront vus en exercices de td/tp.

Planche : 5

Expansion de cond

La forme cond n'est pas essentielle mais bien pratique. Comme elle est utilisée pour écrire l'interprète et que celui-ci doit savoir s'auto-interpréter, elle est définie. Plutôt que de la définir primitivement dans la fonction evaluate comme une forme spéciale additionnelle, on la considère comme une macro que l'on expanse à la volée. La fonction expand-cond est donc l'expanseur (simplifié) associé à cond.

Dans le même genre, il y avait une forme and dans une version précédente de l'interprète qui a été expansée à la main.

(and e1 e2 ...) º (if e1 (and e2 ...))

Planche : 6

Syntaxe abstraite

Pour chaque catégorie syntaxique on a un reconnaisseur (un prédicat) et des accesseurs (qui portent un nom formé du nom de la catégorie syntaxique suivi d'un tiret et du nom du composant extrait). Ils sont tous implantés à l'aide de car, cdr et bien sûr pair?, symbol? etc. On a donc:

variable?
quotation? quotation-data
conditional? conditional-clauses
clause-condition clause-body
alternative? alternative-condition alternative-consequent alternative-alternant
sequence? sequence-forms
local-block? local-block-bindings local-block-body
binding-name binding-form
application? application-operator application-operands
define-form? definition-name definition-variables definition-body

Planche : 7

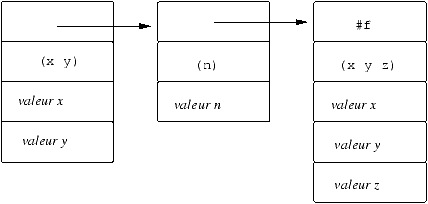
Représentation d'environnements

Classiquement, en Scheme, ce sont des listes d'association mais cela pose un problème pour l'implantation de la récursion mutuelle où l'on a besoin de set-cdr!. On utilisera donc des vecteurs et l'on se permettra d'utiliser vector-set! (qu'un exercice précédent aura introduit). La représentation est fidèle à l'implantation classique par blocs d'activation chaînés.

On a un reconnaisseur empty-environment?, un créateur make-environment, et des accesseurs environment-next, environment-variables, environment-get-value et (en interne pour la récursion mutuelle) environment-set-value!.

Planche : 8

Fonctions environnementales

On peut maintenant définir les fonctions exportables manipulant les environnements: lookup, extend et enrich. Cette dernière correspond à l'extension d'un environnement par des co-définitions mutuellement récursives.

(define (enrich r definitions)
  ;; Environment x Definition* -> Environment
  (let ((names (map definition-name definitions)))
    (let ((frame (make-environment r names)))
      (define (fill! i definitions)
          ;; number x Definition* -> Environment
        (if (pair? definitions)
            (begin
              (environment-set-value!
               frame
               i
               (create-function
                (definition-variables (car definitions))
                (definition-body (car definitions))
                frame ) )
              (fill! (+ i 1) (cdr definitions)) ) ) )
      (fill! 0 definitions)
      frame ) ) )

Dans le cas du code suivant:

(define (test u)
  (define (odd? n)
    (if (= n 0) #f (even? (- n 1))) )
  (define (even? n)
    (if (= n 0) #t (odd? (- n 1))) )
  (even? u) )
(test 813)

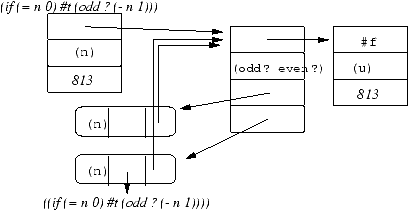
L'environnement où est évalué le corps de (even? 813) est le suivant. On y constate le cycle rendu nécessaire par la codéfinition mutuellement récursive (il existe une solution purement fonctionnelle qui utilise le combinateur paradoxal du l-calcul mais c'est assez compliqué).

Planche : 9

Évaluateur

La fonction evaluate n'est qu'un aiguillage syntaxique sur la fonction spécialisée suivant la catégorie syntaxique: evaluate-variable, evaluate-if, evaluate-begin, etc.

Enfin les itérateurs annexes evlis et eprogn apparaissent. S'y ajoute ebody qui convient à la catégorie syntaxique <body> c'est-à-dire les corps des lambda et des let où peuvent apparaître des définitions locales. ebody ressemble à eprogn sauf qu'elle trie son contenu pour déterminer son corps et les définitions locales qui enrichiront l'environnement lexical courant.

(define (ebody expressions r)
  ;; Expression* x Environment -> Value
  (define (sort-definitions definitions expressions)
    ;; Expression* x Expression* -> Value
    (if (define-form? (car expressions))
        (sort-definitions (cons (car expressions) definitions)
                          (cdr expressions) )
        ;; useless to reverse definitions:
        (eprogn expressions (enrich r definitions)) ) )
  (sort-definitions '() expressions) )

Planche : 10

Représentation des fonctions

Elles sont ici représentées par des fonctions (un exercice est de changer leur représentation par des vecteurs). On y trouve l'invoqueur invoke et le créateur create-function. Le reconnaisseur ne peut encore être défini parce qu'il faut aussi reconnaître les primitives.

Planche : 11

Représentation des primitives

Les primitives sont enveloppées pour apparaître avec la même signature que les fonctions, c'est le rôle de la fonction create-primitive. Les primitives sont reconnues comme les fonctions avec le prédicat function?.

Les primitives sont décrites au moyen de la fonction describe-primitive dont les composantes sont accessibles par les sélecteurs primitive-description-arity etc.

Planche : 12

Environnement global initial

On enrichit l'environnement vide avec un petit utilitaire au-dessus d'extend: augment. Enfin on introduit dans l'environnement initial tout ce qui est nécessaire pour travailler et s'auto-évaluer soit 31 fonctions très exactement. Parmi elles, on notera:

des fonctions ayant une arité variable en Scheme normal et qui revêtent une arité fixe dans le dialecte du deug,
des fonctions d'arité variable (mais les étudiants de deug ne peuvent en créer),
une fonction d'implantation particulière: procedure? qui s'adapte au changement de représentation entre le Scheme interprété et le Scheme interprétant.
une fonction laissée libre, wrong, pour les erreurs (qui sera laissée dans l'ombre).

Planche : 13

(Auto-)interprétation

Pour tester cet interprète sous DrScheme, il faut définir la fonction wrong qui manque puis utiliser la fonction deug-eval.

(define (wrong . culprits) (apply error "DEUG-ERROR:" culprits))
(deug-eval '(+ 2 3))

Voici le code testant l'auto-interprétation:

(define (wrong . culprits) (apply error "DEUG-ERROR:" culprits))
(define eval-definition
  (call-with-input-file "eval3.scm" read) )
(define (eval-deug-eval e)
  (deug-eval `(let ()
                ,eval-definition
                (deug-eval ',e) )) )
(eval-deug-eval '(+ 2 3))

Planche : 14

Conclusions

Quelques chiffres:

501 lignes

286 hors commentaires

31 fonctions primitives

7 catégories syntaxiques

76 définitions

Gammes pour la rentrée:

les exercices du petit polycopié,
les exercices proposés dans plan.html,
et bonnes vacances.

Ce document a été traduit de L^AT_EX par H^EV^EA.