Cours n° 4, 27 octobre 2011
Automates finis déterministes
- I. Notion d'automate
fini et de
langage reconnu par un
automate
- Automate,
algorithme, prédicat
- États et
transitions
- Hypothèse
de finitude
- II. Exemples
- Les
commentaires en C
- Un
exemple scolaire
- III.
Automate minimal
- Observation
sur le rôle des états
- Automate
minimal
- Définition
directe de l'automate minimal à partir du
langage
- Réduction
d'un automate fini
- Visualisation
de la réduction dans le logiciel Automates
- Choix
de l'algorithme
- Démo.
-
Un automate
fini est la représentation d'un algorithme destiné à associer une
valeur booléenne (vrai ou faux) à chaque mot sur
un alphabet X.
En d'autres termes, cet algorithme détermine un
prédicat P portant sur les mots de X*,
c'est-à-dire : pour w ∈X*, P(w) est la
valeur (vrai ou faux) obtenue par l'algorithme quand on l'applique au
mot w,
et par conséquent il définit un sous-ensemble de X*, à savoir L
= {w
∈X* | P(w)},
que l'on appelle le langage reconnu par l'automate.
Le débat porte ensuite sur la manière dont s'exécute l'algorithme en
question,
notamment sur la quantité de mémoire nécessaire en fonction de la
longueur du mot traité.
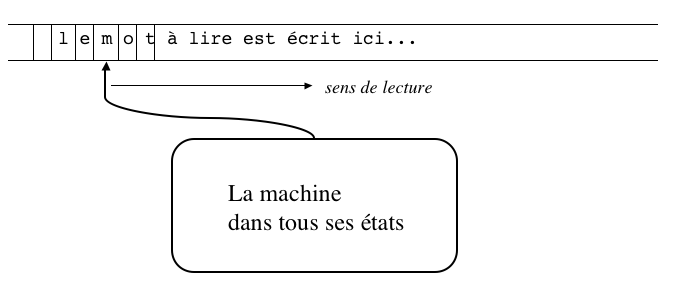
La vision qu'on propose de la mécanisation de cet algorithme est grosso
modo la suivante :
-
-
Lors de l'exécution de cet algorithme, le mot à traiter est lu dans un
sens fixé
(de gauche à droite)
et la valeur vrai ou faux est
obtenue à la fin du calcul.
N.B. du point de vue de la mécanique, la fin du calcul peut avoir lieu
bien après la fin de la lecture,
mais pour simplifier nous supposerons que les deux instants coïncident.
-
À chaque étape, c'est-à-dire après la lecture de chaque lettre
(occurrence)
composant le mot,
on considère que l'algorithme se trouve dans un
certain état.
Cet état matérialise l'information emmagasinée au cours de la lecture
des lettres précédentes,
information qui sera utilisée pour déterminer la valeur
finale.
-
La lecture de la prochaine lettre fera passer l'algorithme dans
un autre état, et ainsi de suite jusqu'à parvenir à la fin du mot.
Ce passage d'un état à l'autre provoqué par la lecture d'une lettre est
appelé une transition.
Nous ferons ici l'hypothèse que les transitions sont instantanées,
c'est-à-dire que la lecture de la prochaine lettre
et le changement d'état qu'elle provoque ont lieu en même temps.
-
À la fin de la lecture, l'algorithme décide de donner une réponse vrai
ou faux en fonction de l'état
dans lequel il se
trouve.
C'est-à-dire que l'ensemble des états est partagé en deux, les états
positifs où la réponse est vrai, les états négatifs
où la réponse est faux.
Les états positifs sont en général appelés terminaux,
ou finals (sic).
Attention ! Ce qualificatif traditionnel doit être compris comme : si
le calcul s'arrête dans un tel état, alors le résultat est vrai,
et non pas comme : le calcul doit
s'arrêter
....
Ce schéma est très général. On le particularise de deux manières :
- soit en imposant l'hypothèse très forte que
l'ensemble des états est fini, ce qui est l'objet de ce cours
- soit, dans le cas contraire, en imposant des
contraintes sur la structure des états et sur les transitions :
l'exemple le plus connu est celui des automates à pile, où chaque état
contient une pile d'informations de taille non bornée.
Nous en parlerons au second semestre.
-
L'hypothèse que l'ensemble des différents états est fini doit
s'entendre au sens fort : un ensemble dont la taille est fixée a
priori,
indépendamment du mot à traiter.
(Sans quoi on pourrait observer que, tout mot étant de longueur finie,
le nombre d'états parcourus au cours de sa lecture est nécessairement
fini,
et que par conséquent l'hypothèse de finitude est toujours
vérifiée ...)
Avec cette restriction, on ne fait aucune hypothèse supplémentaire sur
la nature des états.
En pratique on les identifie à leurs numéros (de 0 à n), ou à des
points du plan dans une représentation graphique.
Les transitions sont données soit sous forme de table, soit sous forme
de flèches étiquetées. Voyez cet exemple.
Après ces explications, nous pouvons formuler la définition classique
d'un automate fini sur un alphabet X,
qui est constitué par
- un ensemble fini dont les éléments sont appelés états
- une fonction de transitions, qui à chaque état et à
chaque lettre de l'alphabet associe un état
- un état initial
- un ensemble d'états terminaux
Notation :
étant donné un état s et un mot w,
on désignera par s.w
l'état atteint par les transitions successives des lettres de w
en partant de s.
Avec cette notation,
- si s0
est l'état initial
- et si T désigne
l'ensemble des états terminaux,
le langage reconnu par l'automate est défini par
: L = {w
∈X* | s0.w
∈T}.
-
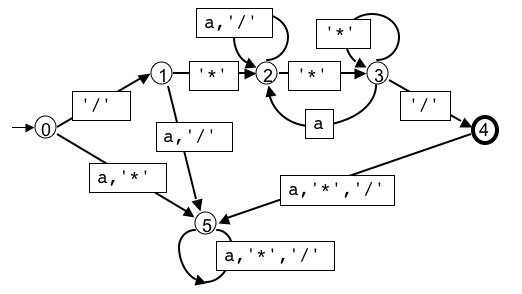
Un automate reconnaissant l'ensemble des mots qui sont des
commentaires
au sens du langage C :
mots commençant par "/*" et se terminant à la
première occurrence de "*/".
Dans la représentation graphique ci-dessous, la lettre "a"
désigne n'importe quel caractère ASCII imprimable
qui n'est ni "/" ni "*".
L'état initial est 0, il y a un seul état terminal qui est 4.
On note la présence d'un état "poubelle" (en anglais sink
= "trou d'évier"),
où aboutissent tous les mots qui ne peuvent pas être prolongés en un
mot du langage
(les mots qui "commencent mal").
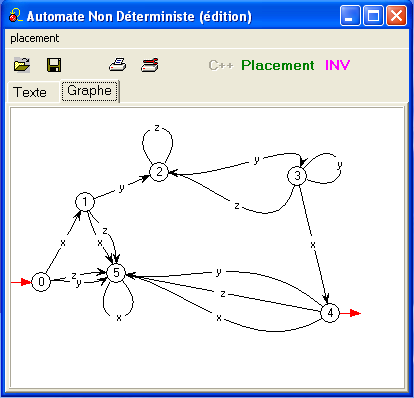
Le même automate représenté dans la fenêtre d'édition graphique du
logiciel Automates,
avec comme convention x = '/', y
= '*', z
= toutes les autres lettres.
La mention Automate Non Déterministe ne doit
pas vous arrêter :
cet automate est parfaitement déterministe, la mention est relative au
processus suivi par le logiciel
(voyez son mode
d'emploi).
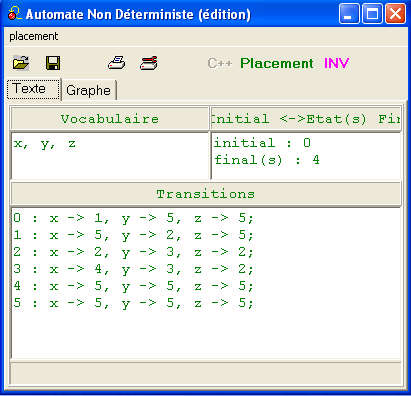
et l'affichage de la table de transitions :
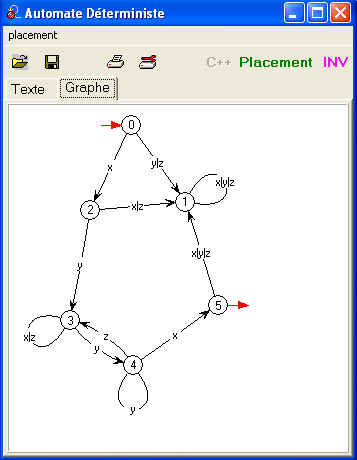
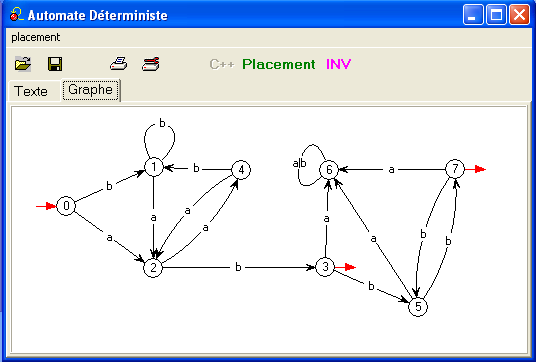
Le même encore représenté dans Automates, après un
prétraitement et avec les conventions relatives aux automates
déterministes :
les sommets ont été renumérotés, les transitions sont indiquées de
manière plus concise.
-
mais commode, emprunté à des notes de
cours de
l'université du Kentucky (claires et intuitives, lecture
recommandée !) .
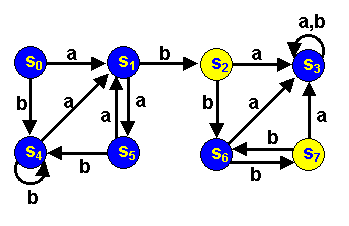
Automate reconnaissant le langage défini par l'e.r. (aa |
b)*ab(bb)*
Dessin original (l'état initial est s0,
les états terminaux sont en jaune, les autres en bleu) :
Ici aussi apparaît un état "poubelle" : après un facteur ab,
on ne peut avoir que des b (en nombre pair),
par conséquent aba n'a aucun espoir de se
voir prolongé en un mot du langage !
Le même vu dans Automates,
en tant qu'automate
déterministe, après
renumérotation des états.
-
On s'intéresse au rôle que jouent les états du seul point de vue de la
reconnaissance du langage.
Comme ils n'ont point d'autre propriété que d'être différents les uns
des autres, on cherche à savoir si cette différence est significative,
où si on pourrait s'en passer sans dommage.
Or, à quoi sert d'avoir deux états différents ? Et d'abord, à quoi sert
un état ?
Un état représente une
certaine information, accumulée au cours de la lecture d'un mot à
partir de l'état initial.
Cette information permet de décider quelles suites données à ce mot
vont aboutir à un état terminal ;
de manière plus formelle :
- soit s un état de l'automate, u∈X*
un mot tel que s0.u
= s
- étant donné un facteur droit v∈X*,
le rôle de s est de décider si s.v ∈T,
c'est-à-dire si le produit uv est dans L
ou non.
Autrement dit, le rôle de l'état s est de discriminer
entre les facteurs droits v qui prolongent u
en un mot de L
et ceux qui échouent.
Ce pouvoir discriminateur est complètement défini par la donnée de
l'ensemble des facteurs qui réussissent : R(s)
= {v
∈X* | s.v
∈T}
[ceux qui échouent forment le complémentaire X*\R(s)].
Dans l'exemple ci-dessus, on obtient comme collection :
- R(0) =
(aa|b)*ab(bb)* le langage
lui-même
- R(1) = R(0), en effet, un
b
peut être suivi par n'importe quel mot du langage, et seulement par un
mot du langage
- R(2) =
b(bb)*|a(aa|b)*ab(bb)*, car
après
un a, soit on passe à la séquence de b
finale, soit on lit un second a qui ramène au circuit
initial
- R(3) =
(bb)*
- R(4) = R(0) = R(1)
- R(5) =
b(bb)*
- R(6) = ∅
- R(7) = R(3) comme il est dit plus loin
Remarque marginale : avec cette définition, on obtient L
= R(s0),
et s∈T
<=> ""∈R(s)
["" = le mot vide].
Deux états s et t tels que R(s)
= R(t) jouent donc le même rôle,
et il est inutile de les distinguer.
Cette observation fondamentale est le point de départ de la théorie de
l'automate minimal.
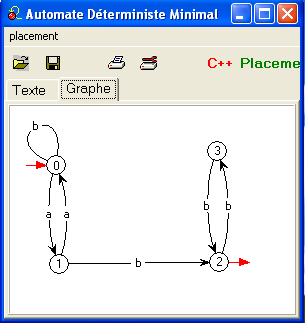
Exemple :
Dans notre second exemple ci-dessus, version Automates,
il est clair que la distinction entre les deux états terminaux 3 et 7
est inutile.
En effet, la différence entre ces deux états disparaît dès la première
transition, que ce soit par a ou par b
:
il est donc certain que 3.w = 7.w
dès que w est non-vide, et comme ils sont tous deux
terminaux, on a bien R(3) = R(7).
-
Étant donné un automate fini, on considère la relation d'équivalence
définie sur l'ensemble de ses états par :
deux états s et t sont
équivalents lorsque R(s) = R(t).
L'ensemble des classes de cette équivalence est en correspondance
bi-univoque (alias bijection)
avec la collection des ensembles R(s),
que l'on appelle les résiduels
(nous verrons plus loin que cette collection dépend uniquement du
langage reconnu, pas de l'automate particulier).
Cette relation a une propriété remarquable de compatibilité avec les
transitions :
si s et t sont équivalents,
alors s.u et t.u
le sont aussi quelque soit le mot u.
[En effet, de la définition de R on tire que R(s.u)
= {f ∈X* | uf
∈R(s)}. Par suite, "R(s)
= R(t)" => "R(s.u)
= R(t.u)".]
Il s'ensuit que l'on peut construire un nouvel automate ayant
- pour états les classes d'équivalence,
- pour transitions celles qui se déduisent de la
propriété ci-dessus
- pour état initial la classe de l'état initial
- pour états terminaux les classes des états terminaux
et que cet automate reconnaît le même langage que l'automate initial.
C'est cet automate que l'on appelle automate minimal.
Exemple scolaire :
nous montrerons plus loin que l'équivalence en question a cinq classes
{0,1,4} / {2} / {5} / {6} /
{3,7}.
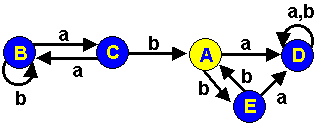
Avec A = {3,7} B = {0,1,4}, C = {2}, D = {6} et E = {5} on
obtient l'automate minimal :
-
La construction précédente dépend de l'automate choisi. Elle ne
justifie nullement que l'on parle de
l'automate minimal au singulier défini. Tout au plus avons-nous trouvé un
automate minimal...
En fait, il n'en est rien !
L'automate minimal est bel et bien unique, lié de manière intrinsèque
au langage
et fournissant une réponse à la question posée au cours 3 d'une
désignation pour les langages.
Pour le voir, il suffit de montrer que l'ensemble des état de
l'automate minimal que nous avons construit
est en bijection avec un autre ensemble défini en toute
indépendance, à partir du langage reconnu.
Définissons pour les mots une variante de la fonction R
que nous avons utilisée pour les états :
posons pour un mot w quelconque : R(w)
= {f
∈X* | wf
∈L}, avec un R
gras pour le distinguer de l'autre.
Les deux notions, la grasse et la maigre, sont reliées par
l'égalité R(w)
= R(s0.w).
La collection des ensembles R(w) est
donc identique à celle des résiduels obtenus ci-dessus avec
l'automate,
mais elle est définie en ne faisant intervenir que le langage L.
Nous pouvons donc l'appeler la collection
des résiduels du langage !
Vu que les états de l'automate minimal sont en bijection avec les
résiduels,
nous obtenons ainsi, comme annoncé, une caractérisation des états de
l'automate minimal à partir du langage seul.
Le reste de la construction s'ensuit (transitions, état initial, états
terminaux).
Ceci nous autorise à parler de l'automate minimal d'un langage, au
singulier défini -
à condition toutefois que ce langage soit effectivement reconnaissable
par un automate fini, ce qui est une autre histoire.
-
Notons que le discours théorique précédent ne nous livre aucun moyen
pour déterminer la collection des résiduels.
Cette collection n'est certes pas plus facile à décrire que le langage
lui-même !
La construction effective de l'automate fini va donc se faire en
partant
d'un automate reconnaissant le langage,
qui nous donne au passage la garantie que ce langage est effctivement
reconnaissable !
La démarche consiste non pas à chercher comment regrouper
les états en classes,
mais à se demander quels états doivent être séparés,
en faisant apparaître un mot qui est dans le résiduel de l'un
mais pas dans celui de l'autre. Ce mot sera construit lettre après
lettre par le procédé suivant.
- On part d'une division de l'ensemble des états en deux
classes : les
états terminaux et les autres.
- Pour chaque lettre de l'alphabet, on examine si elle
sépare deux états
de la même classe,
c'est-à-dire si sa transition envoie le premier dans une classe et le
second dans une autre :
- si tel est le cas, on subdivise la classe en question.
- On répète l'opération jusqu'à ce qu'aucune subdivision
ne se produise plus.
[ Ce qui arrive après au plus n étapes, si n
est le nombre d'états. ]
Ce critère d'arrêt étant vérifié, on voit qu'on peut prendre l'ensemble
des
classes comme nouvel ensemble d'états,
les transitions se faisant désormais de classe à classe (sans risque de
subdivision !).
Ce qui rejoint le raisonnement précédent.
Exemples :
- Dans notre exemple scolaire : initialement deux classes
:
0,1,2,4,5,6 / 3,7.
La lettre b sépare 2 et 5 des autres, d'où
une division en trois classes 0,1,4,6 / 2,5 / 3,7
La lettre a sépare l'état 6 des
autres, d'où une division en quatre classes 0,1,4 / 2,5 / 6 /
3,7
La lettre a sépare les états 2 et 5 entre
eux, d'où une division en cinq classes 0,1,4 / 2 / 5 / 6 /
3,7
Plus aucune séparation n'est possible.
L'équivalence de réduction est donc 0,1,4 / 2 / 5 / 6 /
3,7, comme annoncé plus haut.
- Dans l'exemple des commentaires de C (avec la nouvelle
numérotation) :
initialement deux classes : 0,1,2,3,4 / 5
la lettre x sépare 4 des autres, d'où trois
classes 0,1,2,3 / 4 / 5 ;
la lettre y sépare 3 des autres, d'où quatre
classes 0,1,2 / 3 / 4 / 5 ;
la lettre y sépare 2 des autres, d'où cinq
classes 0,1 / 2 / 3 / 4 / 5 ;
la lettre x sépare 0 de 1, d'où six classes 0
/ 1 / 2 / 3 / 4 / 5.
L'équivalence de réduction est ici l'égalité, l'automate donné était
donc minimal !
-
-
La minimisation des automates finis a été étudiée de très près, d'abord
en raison de son utilité dans la réalisation des compilateurs,
puis en vue des multiples applications des automates finis, notamment
dans le traitement des langues naturelles (en anglais Natural
Language Processing ou NLP).
- Les idées essentielles de la méthode classique
présentée ci-dessus remontent aux années 50 (Huffman, Moore, Nerode).
Avec une implémentation appropriée, elle conduit à un algorithme dont
le temps de calcul croît comme le carré du nombre
d'états (on dit qu'il est "en O(n2)").
- Dès 1962, John
Brzozowski publia une technique entièrement différente, dont
nous parlerons plus tard.
- En 1971, John Hopcroft proposa un
raffinement
de la méthode classique avec un temps de calcul en O(nlog(n)).
Son procédé a été maintes fois commenté, il reste actuellement la
référence.
On en trouve une présentation agréablement animée, sur le
même exemple scolaire qu'ici, dans les planches 10 à 14 de
http://michael.cadilhac.name/public/writings/05-cover-automata-slides.pdf
Automates
propose trois techniques pour réduire un automate
déterministe :
- celle de John Brzozowski : c'est la
technique
adoptée par défaut.
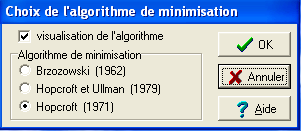
La
documentation du logiciel
contient une page à son sujet : pour la trouver, demandez dans l'index :
automate
> déterministe minimal, ou bien
demandez
de l'aide depuis la fenêtre de dialogue "Choix de l'algorithme...".
- les deux autres sont des variantes de la méthode
classique :
- Hopcroft & Ullman (1979) : se réfère à
la
présentation donnée dans le livre (textbook qui a
fait date !)
Introduction to Automata Theory, Languages and
Computation. Addison-Wesley Publishing Company, 1979.
implémentation en O(n2)
- Hopcroft (1971) : c'est ici l'article original
qui
est cité, implémentation en O(nlog(n)).
Du point de vue de la visualisation, le choix entre les deux
dernières options est indifférent.
-
Nous illustrons la visualisation de la méthode classique avec l'exemple
scolaire.
On part de l'automate déterministe vu
plus haut.
- Dès qu'on lance la réduction (en cliquant sur la
flèche idoine), apparaît une nouvelle fenêtre consacrée à la
visualisation du processus.
Il ne faut pas hésiter à placer proprement l'automate pour suivre le
déroulement !
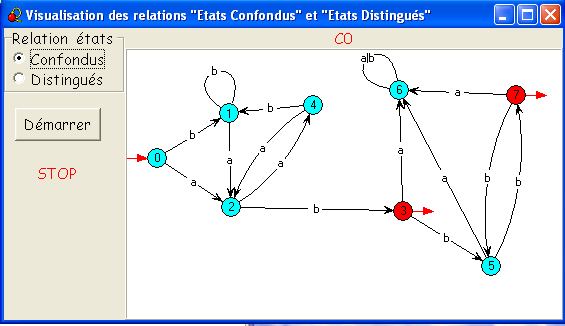
Au commencement les deux classes d'états (0,1,2,4,5,6 / 3,7) sont
identifiées par les couleurs bleu-vert et rouge.
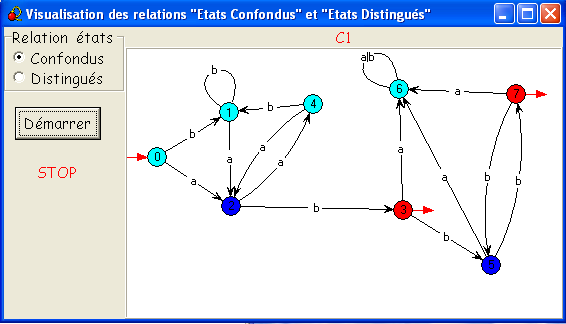
- En cliquant sur Démarrer, on
provoque une première séparation, celle des états 2 & 5, et la
nouvelle classe est colorée en bleu foncé.
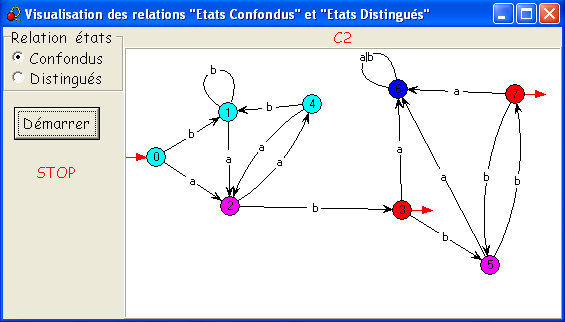
- En cliquant une deuxième fois sur Démarrer,
on provoque la séparation de l'état 6, la nouvelle classe est
colorée en bleu foncé
et la classe précédente est à présent colorée en mauve.
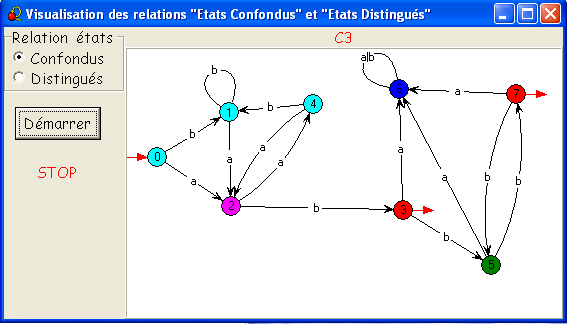
- En cliquant une troisième fois sur Démarrer,
on sépare 2 de 5, celle des états 2 & 5, 2 reste mauve mais 5
devient vert.
- En cliquant une quatrième fois sur Démarrer,
rien ne change au tableau - puisqu'aucune séparation n'est plus posible
-
mais le message "Fini !" vient remplacer le bouton Démarrer.
Il convient alors de fermer la fenêtre de visualisation avant de
demander l'affichage de l'automate minimal (en cliquant
dans le rectangle ad hoc).
On note que dans cet affichage l'état-poubelle a disparu, ainsi que les
transitions qui y menaient.
Le logiciel automate considère en effet que l'absence de
certaines
transitions (ici, les transitions par la lettre a
pour les états 2 et 3)
suffit à indiquer la présence d'un tel état.