Un exemple de manipulation

1. Lecture
   Cette expression se lit  :
   
   1. d'abord un x
   2. puis un certain nombre de y (peut-être aucun)
   3. puis un x
   4. puis un certain nombre de x (peut-être aucun)
   5. enfin un y.
      
      
   Sa valeur est l'ensemble des mots qui peuvent être construits par ce procédé.
   
   
2. Automate
   Nous allons voir à présent comment reconnaître cet ensemble de mots par un automate fini (en anticipant sur la suite du cours)
   
   
   
   
   
   
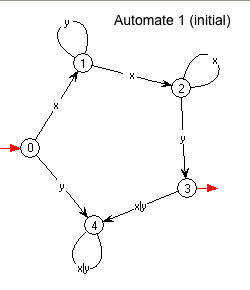
   • Les états sont représentés par des points du plan, porteurs d'étiquettes numérotées pour les identifier (dans de petitis cercles).
     L'état initial, celui dans lequel se trouve l'automate au début de la lecture de la chaîne d'entrée, est signalé par unr flèche entrante rouge.
     L'état terminal, celui dans lequel l'automats doit se trouver à la fin du calcul pour produire le résultat vrai, est marqué par une flèche sortante, rouge également. Il peut y avoir plusieurs états terminaux.
     
   • Les transitions sont indiquées par des flèches d'état à état, portant comme étiquette la lettre de l'alphabet qui déclenche la transition en question.
     
     
   • Un mot est accepté par l'automate si la suite de transitions provoquée par la lecture de ce mot en commençant dans l'état initial se termine dans un état terminal.
     Exemple positif :
      x y y y y x x x y
0 1 1 1 1 1 2 2 2 3
     Exemple négatif :
      x y y y y x x x y x
0 1 1 1 1 1 2 2 2 3 4
     
     
3. Automate inversé
   
   
   1. On l'obtient tout simplement en renversant le sens des flèches des transitions, et en échangeant états initiaux et états terminaux.
      Le langage accepté par cet automate est alors l'ensemble des chaînes obtenues en renversant les chaînes du langage initial.
      Or, même si l'automate de départ était déterministe, il y a de fortes chances pour son inverse ne le soit plus !
      
      
      
      
      
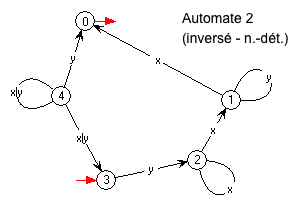
   2. C'est le cas pour notre exemple : dans l'état n°2, la lettre x peut soit boucler sur 2 soit passer à l'état 1 ; de même, dans l'état 4, avec les deux lettres on revient vers 2 ou bien on boucle.
      Voici un automate déterministe équivalent à l'automate non-déterministe précédent, qui reconnaît donc le même langage :
      
      
      
      
      
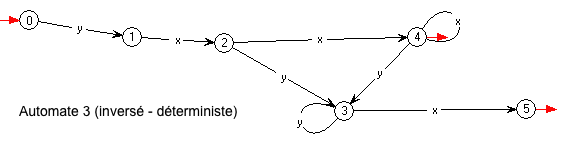
   3. Le langage accepté par cet automate est formé en renversant les chaines produites par le procédé exposé ci-dessus.
      Les chaînes renversées seront produites par le procédé renversé :
      
      1. d'abord un y
      2. puis un certain nombre de x (peut-être aucun)
      3. puis un x
      4. puis un certain nombre de y (peut-être aucun)
      5. enfin un x. 
         
      Il sera donc décrit par l'expression régulière qui traduit ce procédé :  yx*xy*x
      
      
4. Une autre expression régulière pour le langage inversé
   
   À partir de l'automate 3, la machine (le logiciel automate) calcule l'expression : yxxx* | yxyy*x | yxxx*y+x .
   
   Dans cette écriture, la barre verticale "|" désigne l'union des ensembles.
   Sachant que l'opérateur postfixé "+" signifie "un nombre quelconque, non nul", et que l'on peut donc poser y+ = yy*
   pour revenir à nos notations antérieures, nous aboutissons à l'égalité :
   
   
   yx*xy*x (notre calcul) = yxxx* | yxyy*x | yxxx*yy*x (calcul de la machine)
   
   Sommes-nous bien sûrs que cette égalité soit valable ? que personne ne s'est trompé ?