Langages réguliers et hors-contexte Cours M1 INaLCO, 20010-2011
Interrogation écrite du 07/12/2010 : Corrigé
L'énoncé.
-
Première partie
On considère un alphabet à deux lettresaetb, et l'automate suivant sur cet alphabet :
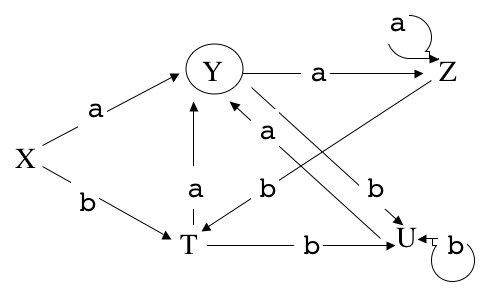
Les états de l'automate sont étiquetés X, Y, Z, T et U, l'état initial est X, le seul état terminal est Y.
Appelons A cet automate.
- L'automate A est-il
déterministe ?
Oui, car- à chaque état et à chaque lettre de l'alphabet est associée une transition et une seule
- il n'y a pas d'ε-transition
Si oui, donnez sa table de transitions.
a
b
X
Y
T
Y
Z
U
Z
Z
T
T
Y
U
U
Y
U
- L'automate A est-il minimal ?
Non, car les états T et U ont le même avenir :Si non, réduisez-le et donnez l'automate minimal qui reconnaît le même langage.
- avenir immédiat (effet du mot vide) : ni l'un ni
l'autre n'est terminal ;
- avenir commençant par
a: l'un et l'autre passent par Y ;
- avenir commençant par
b: l'un et l'autre passent par U .
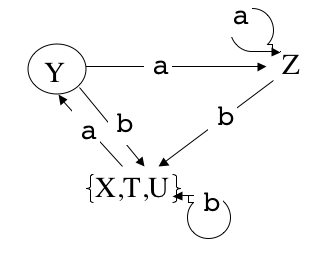
- Du fait que T et U sont équivalents (cf. supra) suit que X est aussi dans la même classe d'équivalence (même raisonnement) :
- On ne peut pas réduire davantage, car Y étant terminal
est séparé des autres par le mot vide, et Z est séparé par
a
[{X,T,U}.a= Y est terminal, Z.a= Z ne l'est pas].
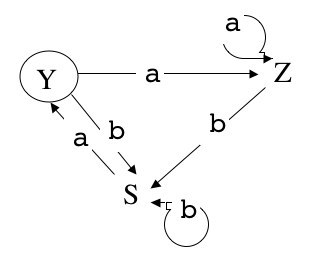
et en renommant les états (S initial, Y terminal)
- avenir immédiat (effet du mot vide) : ni l'un ni
l'autre n'est terminal ;
- Donnez une expression régulière décrivant le langage
reconnu
par l'automate A .
Il s'agit de décrire les mots qui mènent de S à Y. Appelons L l'ensemble de ces mots.
Comme la seule transition qui conduit à Y est la transition S.a= Y, tout mot w menant de S à Y est de la forme
w = ua, où u conduit de S à S, et réciproquement tout mot de cette forme est accepté par l'automate.
Donc L = Ca. où C est l'ensemble des mots u tels que S.u = S.
(En théorie des graphes, on parlerait des circuits autour du sommet S.)
Reste à décrire l'ensemble C.
Il est clair qu'un tel mot est de la forme u = u1u2...uk, où chaque ui va de S à S sans repasser par S (circuits élémentaires),
de sorte que C = E*, où E est l'ensemble des mots qui conduisent de S à S sans repasser par S.
Ce dernier ensemble est facile à décrire :b | ab | aaa*b.
Cette analyse nous donne pour le langage L l'expression régulière(b | ab | aaa*b)*a.
Une autre analyse nous aurait conduit à une autre expression...
- L'automate A est-il
déterministe ?
-
Deuxième partie
On considère l'automate B non-déterministe à 5 états I, II, III, A, B, où I est l'état initial et I, III, B les états terminaux.
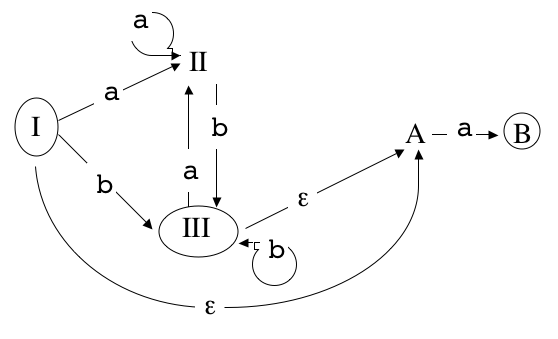
- Que pouvez-vous dire du langage reconnu par l'automate B ?
En d'autres termes, donnez a priori une forme d'expression régulière pour ce langage.
L'intention de l'auteur de l'énoncé était de faire apparaître que le langage reconnu par B était
le langage reconnu par l'automate C de la question suivante concaténé avec la lettrea,
en retrouvant la structure décrite dans le cours 5.
Malheureusement, dans son désir de mettre en évidence la structure en question,
il a oublié d'indiquer que les états terminaux de C, d'où sont issues les ε-transitions vers A,
ne sont plus terminaux dans l'automate reconnaissant le produit !
D'où une confusion regrettable...
L'automate aurait dû être D , avec I initial et B seul état terminal :
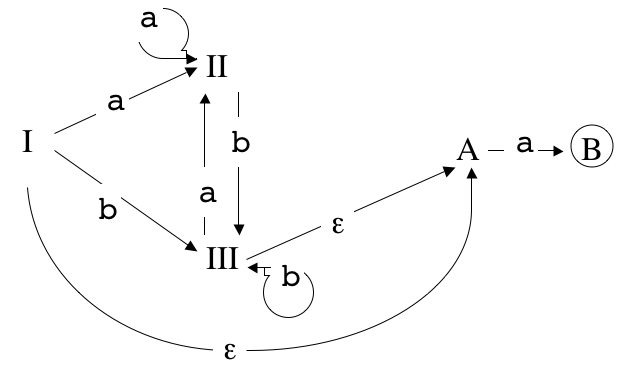
Appelons B (resp. C, D) le langage reconnu par l'automate B (resp. C, D).
La réponse attendue était D = Ca.
L'automate B étant ce qu'il est (et non ce qu'il devait être), la réponse correcte est B = C | Ca.
- Reste à déterminer le langage reconnu par l'automate C que voici
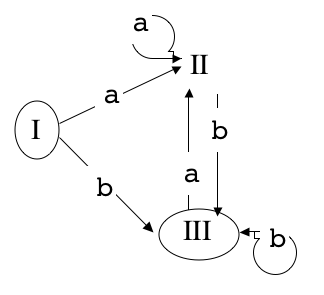
Vérifiez que(a*b)*=Σ*b ∪ {ε}, oùΣdésigne l'alphabet{a, b}, cela peut vous aider...
L'idée est que l'automate C reconnaît "évidemment" le langageΣ*b ∪ {ε} :
- l'état initial et terminal I correspond au mot vide, et
à lui seul puisqu'aucune transition ne revient en I ;
- les mots conduisant de I à III se terminent tous
par
b, car les seules transitions arrivant en III sont effectuées parb; - réciproquement tout mot se terminant par
barrive en III.
Quant à la vérification demandée, elle repose sur l'observation suivante :
- tout mot non vide de
(a*b)*se termine parb; on a donc(a*b)*⊆Σ*b ∪ {ε} - tout mot se terminant par
bpeut s'écrire comme un produit de facteurs de la formeakb, avec k>=0
[il suffit de "couper à chaque occurrence deb" : entre deux occurrences consécutives deb, il n'y a que desa...],
le mot en question est donc dans(a*b)*, ce qui prouve l'inclusion opposée.
(a*b)*.
- l'état initial et terminal I correspond au mot vide, et
à lui seul puisqu'aucune transition ne revient en I ;
- Montrez que l'automate déterministe associé à l'automate B n'est autre que l'automate A qui a été envisagé dans la première partie.
La structure de l'automate déterministe associé à B ne dépend pas du choix des états terminaux.
Le résultat sera donc le même si on part de B ou de D.
La construction indiquée dans le cours 5 appliquée à D donne :
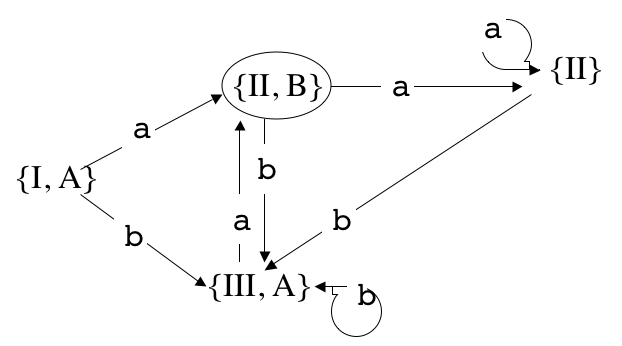
qui en renumérotant les états ne donne pas exactement l'automate A,
mais l'automate obtenu après un pas de réduction (T, U),
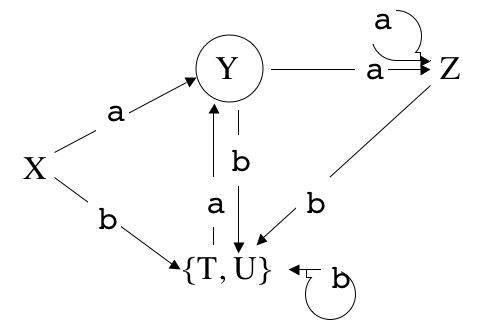
et qui aboutit au même automate minimal et reconnaît donc le même langage que A.
Pouvez-vous en déduire une autre réponse à la question I.3 ?
L'intention était clairement de raisonner sur D et d'aboutir à L =(a*b)*a.
La question perd son sens vu l'erreur sur les états terminaux de B...
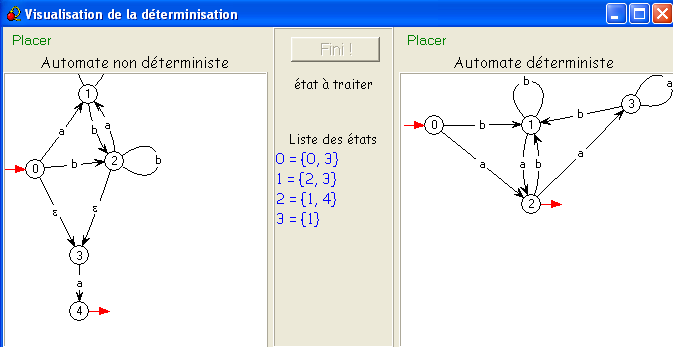
Voici la séquence obtenue avec automate en partant de l'automate non-déterministe D :
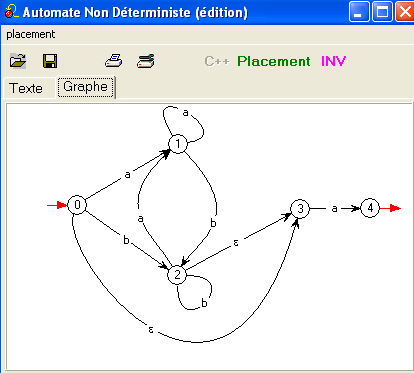
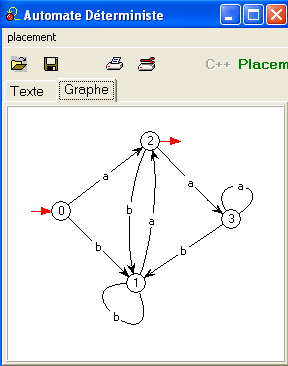
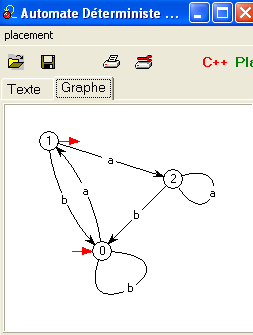
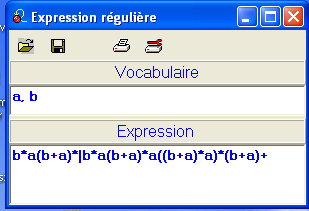
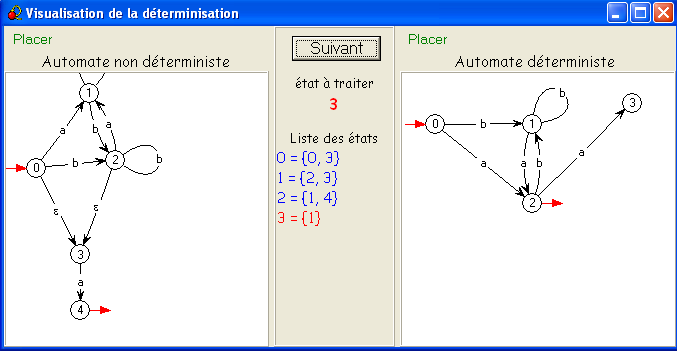
Encore une autre expression pour notre langage apparemment si simple ! Détail du calcul.
Voici le détail de la "déterminisation" de D :
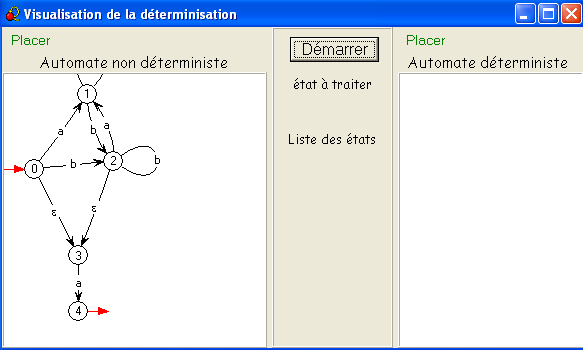
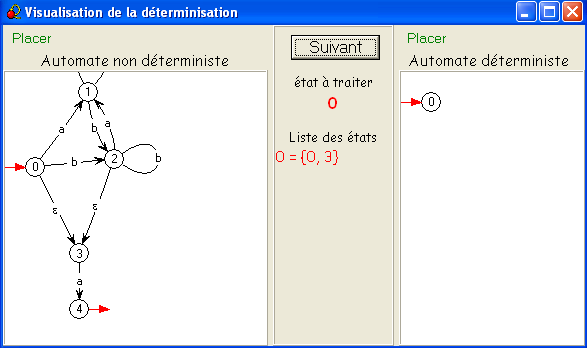
On voit qu'il considère immédiatement une ε-transition applicable à l'état initial,
de sorte que le nouvel état initial est {0, 3}.

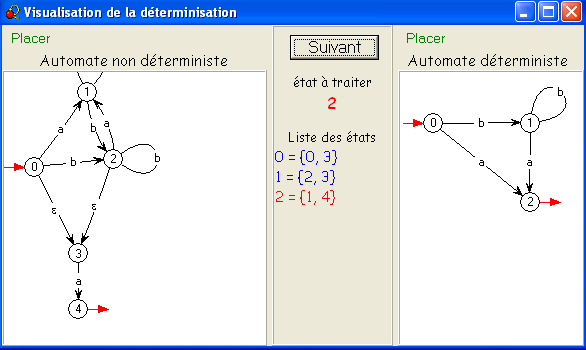
- Que pouvez-vous dire du langage reconnu par l'automate B ?