Cours n° 5, 24 octobre 2013
Automates finis non-déterministes
Tout langage régulier est reconnaissable par un automate fini
- Notion
d'automate non-déterministe
- Prologue
- Principe
- Exemple
: Renverser un automate
- Constatation
: ce modèle plus général n'est pas plus puissant
que le modèle déterministe
- Construction
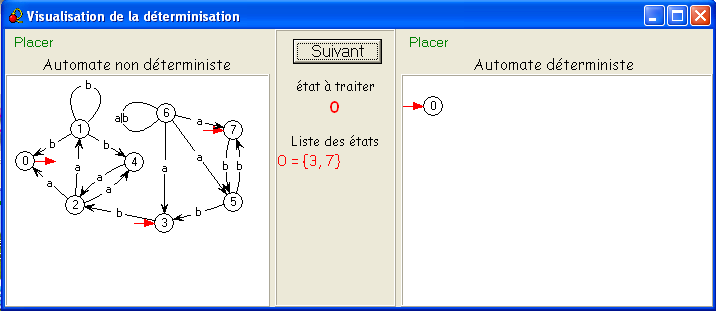
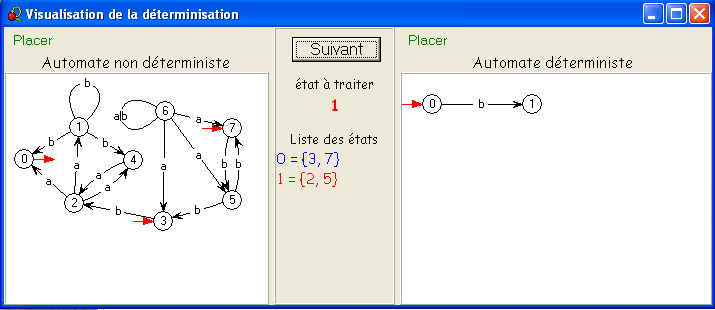
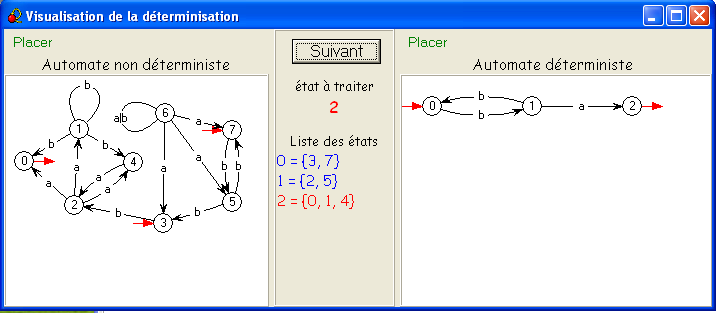
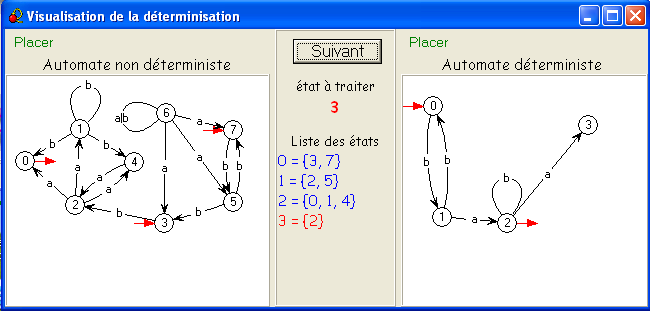
- Visualisation
de la déterminisation dans le logiciel automate.
- Propriétés
de fermeture de la classe des langages
reconnaissables par automates finis
- Fermeture
par passage au complémentaire
- Fermeture
par image-miroir
- Fermeture
par union ensembliste
- Fermeture
par produit (concaténation) des langages
- Fermeture
par itération (étoile)
- Conclusion
- Inclusion
- Lemme de
l'étoile
- Application
-
En théorie des automates, le non-déterminisme joue un rôle central.
Il est utile de réfléchir à ce rôle, d'autant plus qu'un automate
non-déterministe est un animal bien différent d'un automate
déterministe,
comme l'observe justement Jacques Sakarovitch :
En fait, les automates déterministes sont de structures d'une
autre
nature que les automates généraux.
[Éléments de Théorie des Automates, p. 110].
C'est que le non-déterminisme apparaît dans le modèle du
processus envisagé,
tandis que l'automate déterministe intervient comme une implémenttion
(programmation) de ce modèle.
Exemple : envisageons le problème de la reconnaissance des palindromes (du genre "roma summus amor"),
en exigeant de procéder en une seule passe de gauche à droite
(ce qui
interdit de connaître la longueur du mot-candidat avant la fin du
processus).
Le modèle traditionnel utilise une pile où (1) la première moitié du
mot est logée,
puis (2) extraite en ordre inverse pour contrôler la correspondance
lettre à lettre avec la seconde moitié.
Comme rien n'indique à quel endroit se trouve le milieu du mot, la
décision de passer de la phase (1) à la phase (2)
est non-déterministe... et ce modèle n'est pas implémentable !
Le résultat principal de ce cours-ci est en somme que
tout modèle (non-déterministe) où le nombre d'états qui intervient est fini
peut se programmer par un automate fini (déterministe).
Il trouvera son application principale dans la solution des problème de
factorisation :
- Étant donné un mot w, trouver s'il existe une
factorisation w = uv, où u est dans un certain
langage P et v dans un autre Q
(c'est-à-dire, reconnaître le langage produit PQ)
- Étant donné un mot w, trouver s'il existe une
factorisation w = u1u2u3....uk,
où tous les ui sont dans un certain langage P
(c'est-à-dire, reconnaître le langage P*)
Dans ces deux cas, c'est la question de l'existence d'une factorisation
qui est la source du non-déterminisme du modèle.
Et nous verrons que, si les langages P et Q sont
reconnaissables par des automates finis,
le modèle non-déterministe ne fait appel qu'à un nombre fini d'états,
et peut donc se réaliser par un automate fini (déterministe).
-
Dans le modèle d'automate que nous avons étudié
au cours
n°4, étant donné un état s et une lettre
de l'alphabet
x,
il y a exactement
une transition de s par x,
aboutissant à un sommet bien déterminé.
Le calcul de l'automate est déterministe en un sens
facile à comprendre.
Il est moins facile de se faire une idée intuitive
d'un calcul non-déterministe...
- Plusieurs transitions possibles
par
la
même lettre pour un
même état, donc plusieurs résultats possibles.
La fonction de transitions t prend donc ses valeurs
dans les parties de l'ensemble des états :
si S désigne l'ensemble des états, pour une lettre x
et un état s, on a t(x, s)
⊆ S et non
plus t(x, s) ∈ S.
- Le cas échéant, pas de transition, ce qui
correspond
à t(
x, s) = ∅.
- Possibilité de transitions d'état à état
sans lire une
lettre, ou transitions spontanées, alias ε-transitions,
ou transitions
par le mot vide.
Cette faculté vient compliquer le calcul des transitions lors de la
lecture d'un mot !
Il faudra à chaque pas tenir compte des ε-transitions qui peuvent se
produire...
Nous définirons donc t(x, s) ⊆ S
comme l'ensemble
des
états qu'on peut atteindre à partir de s par
- une première suite (éventuellement
vide)
d'ε-transitions,
- une transition par
x
- une seconde suite (éventuellement
vide)
d'ε-transitions.
Dans tous les cas, on arrive à l'idée qu'un
même mot
appliqué à un même
état peut donner naissance à plusieurs calculs,
aboutissant à plusieurs états différents. Pour faire bonne mesure, on
accepte aussi d'avoir plusieurs états initiaux.
Il va de soi que la notion ainsi esquissée (nul besoin d'une définition
en forme !) est plus générale que celle d'automate fini déterministe,
et que par conséquent, même si cet énoncé choque le sens commun, tout
automate fini déterministe est aussi non-déterministe !
Dans ces conditions, la notion de langage reconnu par l'automate est
définie d'une manière plus souple :
c'est l'ensemble des mots pour lesquels on peut trouver
un état
initial, et un calcul du mot à partir ce cet état
qui aboutit à un état
terminal.
Clairement, cette définition élargie revient exactement à la
précédente si l'automate visé se trouve être
déterministe.
Répétons : c'est ce on peut trouver qui signe le non-déterminisme.
Or, il fait souvent partie de l'énoncé du problème à traiter... Il s'agit alors de trouver les états.
-
Étant donné un langage L, on considère le langage L~
formé des mots de L lus dans l'autre sens (en
pratique, de droite à gauche).
Cette inversion du sens de lecture est souvent appelée l'image
dans un
miroir, ou image-miroir, et notée avec le tilde comme
opérateur unaire.
On note donc L~ = {w~
| w ∈L}.
On observe que cette opération effectuée deux fois de suite revient à
l'identité : (w~)~ = w.
Si L est reconnu par un automate fini A
(déterministe ou non) alors L~ est reconnu par
l'automate fini A~ (très probablement
non-déterministe)
obtenu en prenant
- le même ensemble d'états que A
- les transitions inverses de celles de A,
c'est-à-dire que
la lettre x fait passer de
l'état s à l'état t dans A~
si et seulement si elle fait passer de t à s
dans A.
- comme états initiaux, les états terminaux de A
- comme états terminaux, les états initiaux de A.
En effet, les calculs de A~
reproduisent exactement ceux de A
"à l'envers", si bien qu'un mot w est accepté par A~
si et seulement si son image-miroir w~ est acceptée
par A.
C'est cette opération qu'effectue l'option INV
dans le
logiciel Automate.
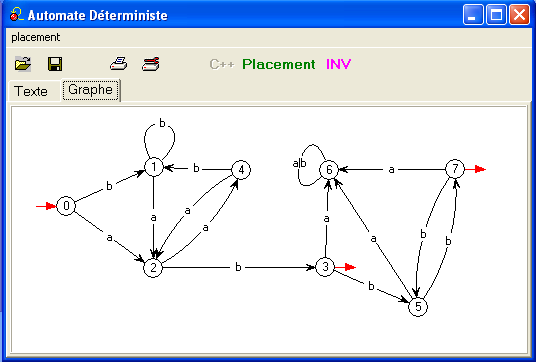
Elle fait passer, par exemple, de l'automate déterministe de notre
exemple scolaire (cours
n° 4), que voici :
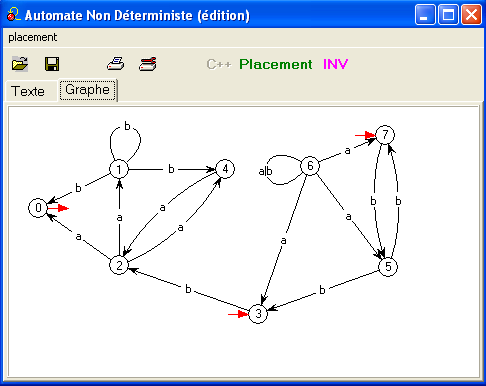
au suivant qui est clairement non-déterministe
(le placement a été légèrement modifié pour faire apparaître les
flèches rouges sur 3 et 7 qui ont changé de sens)
Pour tout langage reconnu par un automate fini
non-déterministe, on sait construire un automate fini déterministe qui
le reconnaît.
Soulignons que cette propriété et l'apanage des automates finis. Elle
cesse d'être vraie pour les autoltates à pile, etc.
-
Cette construction est très facile :
étant donné N un automate fini
non-déterministe donné par
- son ensemble d'états S
- sa fonction de transitions t ,
y
compris d'éventuelles ε-transitions
[ on rappelle
que pour toute lettre x et
tout état s, t (x, s) est
une partie de S
ainsi que t (ε, s) - au besoin relisez...]
- son ensemble d'états initiaux I
- son ensemble d'états terminaux T
on construit l'automate déterministe équivalent D
en prenant
- comme ensemble d'états, l'ensemble des parties de S
(ou plus précisément, l'ensemble des parties de S accessibles
au sens qu'on va voir plus loin) ;
- comme fonction de transitions : la fonction d
qui à une lettre
x
et à une partie Q de S associe d
(x, Q)
⊆ S
qui est l'ensemble des états s de N
pour lesquels il existe un état q∈Q
et une transition par x
allant de q à s,
compte-tenu des ε-transitions, c'est-à-dire la réunion des
sous-ensembles t (x,
q) pour q∈Q.
- comme état initial, l'ensemble I
des
états initiaux de N ;
- comme états terminaux, les parties de S
qui contiennent au moins un état terminal de N,
à savoir { R ⊆ S | R∩T
≠ ∅ }.
Précisons maintenant qu'une partie de S sera accessible
si on peut l'atteindre en partant de I par une
suite de transitions au sens de la fonction d.
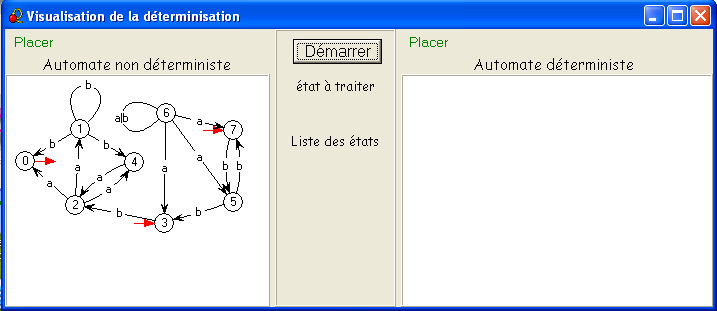
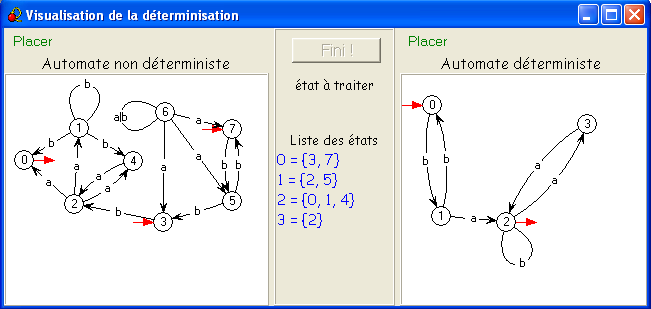
Notre exemple scolaire inversé illustre parfaitement cette idée : S
= {0,1,2,3,4,5,6,7},
on
part de I = {3,7}
- {3,7}.
a =
∅,
{3,7}.b = {5,2},
- {5,2}.
a =
{0,1,4}, {5,2}.b =
{3,7},
- {0,1,4}.
a =
{2}, {0,1,4}.b
= {0,1,4},
- {2}.
a =
{0,1,4}, {2}.b
= ∅.
Seuls quatre sous-ensembles de S (sur 28
= 256) sont donc accessibles : {3,7}, ∅, {5,2}, {0,1,4} et {2}.
L'état ∅ est clairement une poubelle, on peut se dispenser de
le dessiner (avec les conventions
d'affichage du
logiciel automate)
En numérotant 0 = {3,7}, 1 = {5,2}, 2 = {0,1,4}, et 3 = {2}, on obtient
Répétons : soit Q ⊆ S un état
accessible de l'automate D, et w
un mot qui y conduit : d (w, I)
= Q.
Alors Q est l'ensemble des états q
de N pour lesquels il existe un
état initial i ∈I et un calcul de N
par w qui conduit de i à q.
En formule : Q = { q∈S
| ∃i ∈ I, q ∈ t (i , w)
}.
Exemple : Q = {0,1,4}, w = ba
: à partir de I = {3,7}, on a 3. ba
= {0,1,4} et 7. ba
= ∅, d'où {3,7}. ba
= {0,1,4}∪∅ = {0,1,4}.
On peut dire en somme que les différents états élémentaires qui
composent un "macro"-état Q sont indistinguables
du point de vue du calcul :
pour un mot w et deux
états q' et q" de Q,
s'il existe un état initial (élémentaire) i et un
calcul de N tel que i.w
= q',
alors il existe aussi un état j ∈I
(peut-être le même que i ) et un calcul de N
tel que j.w = q".
Par conséquent, il suffit de l'existence d'un
état (élémentaire) q∈Q,
d'un état initial (élémentaire) i, d'un
mot w et d'un calcul de N
tel que i.w = q,
pour assurer que tous les états (élémentaires) qui
forment le macro-état Q sont aussi atteints par un
calcul de N avec le
même mot w à partir d'un état initial
(élémentaire).
En particulier,
- si le macro-état Q contient un
état (élémentaire) terminal r ∈T,
alors pour tout w
- l'existence d'un i ∈I
et d'un calcul de N tel que i.w∈Q
(quel qu'il soit)
- garantit l'existence d'un j ∈I et
d'un calcul de N tel que j.w = r,
- donc que le mot w est accepté par
l'automate non-déterministe N.
Réciproquement, si Q ne contient aucun état
terminal, soit un mot w, i ∈I
et un calcul de N tel
que i.w∈Q,
aucun calcul de N ne va conduire
à accepter w, et w ne fait donc
pas partie du langage reconnu par N.
Pour arriver à l'équivalence désirée, les états terminaux de notre
automate déterministe D doivent
donc être
- non pas le seul ensemble T des
états
terminaux de l'automate non-déterministe N,
- mais bien l'ensemble des parties accessibles de S
qui contiennent au moins un état terminal de N.
Tel qu'il est défini, notre nouvel automate D,
qui est
déterministe par construction, reconnaît donc le même
langage que N, comme annoncé.
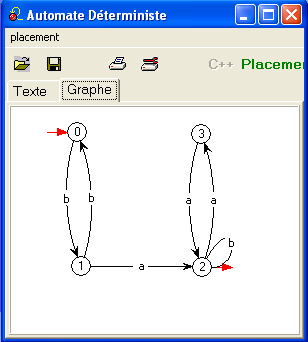
-
Il s'agit du même exemple que celui
qui
vient d'être traité à la main.
-
Évident : si L est reconnu par un automate
déterministe [S, t, s0, T ],
alors son complémentaire X*\L est reconnu par "le
même automate",
avec comme ensemble d'états terminaux le complémentaire de l'ensemble
initial,
à savoir l'automate [S, t, s0, S\T
]
-
Immédiat : si L est reconnu par un
automate déterministe [S, t, s0, T
],
alors L~ est reconnu par l'automate renversé,
non-déterministe [S, t~, T,
{s0} ],
qu'il suffit de rendre déterministe par la construction précédente.
Une illustration de ce processus est donnée dans le mode d'emploi du
logiciel automate, exemple
2.
-
Si L' est reconnu par un automate déterministe [S', t',
s'0, T' ],
et si L" est reconnu par un automate déterministe [S", t",
s"0, T" ],
alors L'∪L" est reconnu par
l'automate déterministe [S'×S", t'×t",
(s'0, s"0)
, T'×S"∪S'×T"
], où
- S'×S" est
l'ensemble des couples (s', s")
avec s'∈S' et s"∈S"
(alias produit cartésien de S'
et de S"),
- t'×t"est
la fonction de transitions qui par la lettre
x
associe à l'état (couple) (s', s") l'état
(couple) (t' (x,
s'), t" (x,
s")),
- l'état initial est le couple des états initiaux des
deux automates
- les états terminaux sont les couples qui ont au moins
une de leurs deux composantes qui est terminale.
En somme, on fait fonctionner les deux automates "en
parallèle",
et à la fin du calcul on regarde si l'un des deux états atteints est
terminal.
Corollaire : fermeture par intersection
(en vertu de la fermeture par complémentation et des lois de de Morgan).
On peut aussi le voir directement, par la même construction "en
parallèle" que ci-dessus,
en prenant pour ensemble terminal T'×T",
l'ensemble des couples dont les deux composantes sont terminales.
-
Si L' est reconnu par un automate déterministe A'
= [S', t', s'0, T' ],
et si L" est reconnu par un automate déterministe A"
= [S", t", s"0, T" ],
(en supposant que les deux ensembles d'états sont disjoints, ce qui est
toujours possible, au prix d'une duplication)
alors L'.L" est reconnu par
l'automate non-déterministe N
ainsi conçu :
- on prend comme ensemble d'états la réunion S'∪S"
- on définit la fonction de transitions ainsi :
- pour les états de A",
on garde t"
- pour les états de A' qui
ne sont pas terminaux, on garde t'
- pour les états de A' qui
sont terminaux, on garde t' et on ajoute une
ε-transition vers s"0
ce sont ces ε-transitions supplémentaires qui rendent l'automate
non-déterministe
- il y a un seul état initial, qui est celui
de A'
- les états terminaux sont ceux de A".
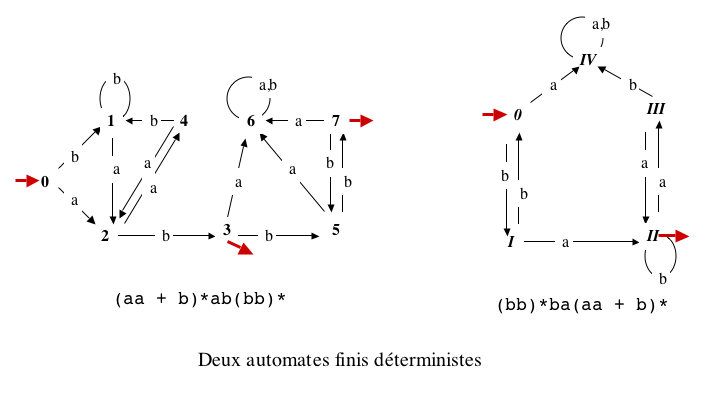
Illustration avec d'une part l'exemple scolaire (non
réduit),
d'autre
part son renversé minimal (ci-dessus),
où on a renommé les états et mis en évidence l'état-poubelle
pour avoir la même convention de représentation dans les deux cas.
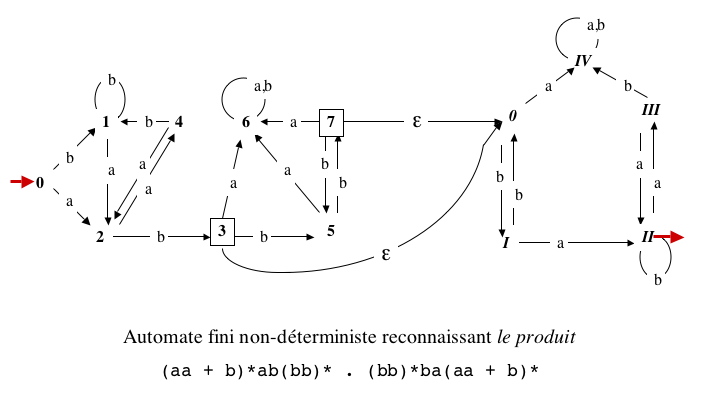
Justification :
- Soit u∈L', v∈L"
et uv leur produit. Il existe un calcul de N
qui accepte uv,
composé du calcul de A' qui
accepte u et se termine dans T',
suivi d'une ε-transition qui arrive à s"0,
suivi du calcul de A" qui
accepte v et se termine dans T",
qui est l'ensemble des états terminaux de N.
- Réciproquement, soit w un mot
accepté par N. Alors il
appartient au produit L'.L".
En effet, le calcul de N qui
l'accepte commence par s'0 (seul
état initial) et se termine dans T",
et comme les deux ensemble S' et S"
sont disjoints, le calcul a dû quitter S' pour passer dans S",
ce qui ne peut se faire que par une ε-transition entre T'
et s"0.
Soit alors u le facteur gauche de w lu avant
ladite ε-transition, et v le facteur droit qui le complète :
on a w = uv, u
arrive dans T' en partant de s'0,
il est donc accepté par A', d'où u∈L',
et v arrive dans T" en partant
de s"0, il est donc
accepté par A", d'où v∈L",
et enfin uv∈L'.L".
Notons au passage que u ou v ou
les deux peuvent être vides.
-
Si L est reconnu par un automate
déterministe A = [S, t, s0,
T ],
alors L* est reconnu par l'automate
non-déterministe N que voici :
- on prend comme ensemble d'états S
auquel on adjoint un nouvel état d
- on définit la fonction de transitions ainsi :
- d n'a qu'une transition, qui est
une ε-transition vers s0
- pour les états qui
ne sont pas terminaux, on garde t
- pour les états qui sont terminaux, on garde t et
on ajoute une ε-transition vers s0
ici aussi, ce sont ces ε-transitions
supplémentaires qui rendent l'automate non-déterministe
- il y a un seul état initial, qui est d
- les états terminaux sont ceux de T,
auxquels on ajoute l'état initial d.
Illustration (suite)
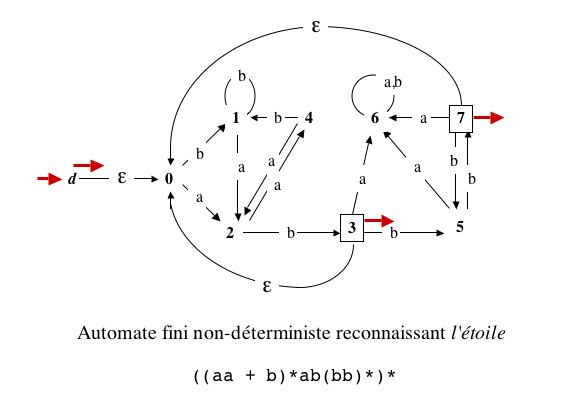
Justification
- Soit w un mot de L*
; s'il est vide, il est accepté puisque l'état initial d
est aussi terminal.
sinon, si c'est un seul mot de L, il est
accepté par une ε-transition initiale vers s0
suivie par un calcul de A
conduisant à un état terminal,
et si c'est un produit d'au moins deux mots de L,
après la lecture du premier une ε-transition ramène à s0
et ainsi de suite (si vous voulez un raisonnement en forme, procédez
par écurrence sur le nombre de facteurs du mot w).
- Réciproquement, soit w un mot
accepté par N. S'il est vide, il
est dans L*.
Sinon, c'est qu'il est accepté via un calcul conduisant à un état de T,
puisque l'état initial d ne reçoit aucune
transition.
Ce calcul a dû commencer par une ε-transition vers s0,
et se poursuivre avec un certain nombre de calculs de A
suivis d'ε-transitions vers s0 (les
seules transitions possibles en dehors de celles de A).
Comme ces ε-transitions ne sont possibles qu'à partir des états
terminaux de A, elles réalisent
une factorisation de w
dont tous les facteurs sont acceptés par A.
Le mot-candidat w est donc dans L*.
Remarque : en général, afin d'accepter le mot vide on
ne
peut
pas faire de s0 un
état terminal du nouvel automate,
et il est indispensable d'isoler un nouvel état initial ne recevant
aucune transition,
comme le montre un exemple comme L = x*y
:
l'automate "naturel" a une boucle par x
sur s0, si bien qu'en
faisant de s0 un
état terminal,
on accepte du même coup tous les x, xx, xxx,
etc...
-
Attendu que la classe des
tous
les
langages
réguliers (valeurs
d'expressions régulières) a été caractérisée comme
la classe des langages réguliers est la plus petite
classe de langages qui
- contient tous les singletons de lettres
- est fermée par les trois opérations d'union, de
concaténation (ou produit) et d'étoile.
et que les les singletons de lettres sont (aisément)
reconnaissables par des automates finis,
et que la classe des langages reconnaissables par des automates finis
est
fermée par les trois opérations d'union, de concaténation (ou
produit) et d'étoile. comme nous venons de le voir
il s'ensuit que
la classe des langages réguliers est contenue dans
celle des
langages reconnaissables par des automates finis,
ou en d'autres termes
tout langage régulier est reconnaissable par un
automate fini.
Reste à démontrer la réciproque !
Mais
ce résultat nous suffit
- pour construire un automate fini à partir d'une
expression
régulière (voir notre premier exemple)
- nous reviendrons sur cette construction
- pour établir que certains langages ne sont pas
réguliers,
en prouvant qu'ils ne sont pas reconnaissables par automates
finis.
-
(en anglais Pumping Lemma)
Si un langage L reconnu par un automate fini A
est infini,
alors tout mot suffisamment long de L contient un
facteur non vide qui peut être répété un nombre arbitraire de fois
sans sortir du langage.
Si l'automate A a n
états, suffisamment long signifie de
longueur supérieure à n.
Vérification
Soit w = x0x1x2...xn...
un mot de L de longueur au moins n+1:
comme l'automate n'a que n états, on est sûr que le
calcul passe au moins deux fois par le même état, appelons-le s
d'où une factorisation de w en w
= f.u.g, où u n'est pas vide,
avec s0.f
= s, s.u
= s
et s.g = s.w.
Le fait que u envoie l'état s
sur lui-même a pour conséquence que tout son itéré u*
aura la même propriété,
si bien que s0.fukg
= s0.w
quel que soit k >=0.
Et si w est accepté par l'automate, il en sera de
même pour tous les autres.
On aura donc f.u*.g
⊆L - d'où le nom familier de ce lemme.
Dans Wikipédia vous trouverez une
intéressante discussion sur le caractère nécessaire mais non suffisant
de cette propriété.
-
Le langage dont les mots sont de la forme "un certain
nombre
de
x,
suivis du même nombre de y",
à savoir L = { xnyn
| n >= 0 }
n'est pas reconnaissable par un automate fini, il n'est donc pas
régulier.
En effet, dès que n dépsse le nombre d'états de
l'automte supposé, on peut "pomper des x"
- et aussi bien "pomper des y"
ce qui ruine l'espoir d'égalité.
Si on interprète x comme
la parenthèse ouvrante et y comme
la parenthèse fermante, cet argument montre que
le langage des systèmes de parenthèses n'est pas régulier, comme nous
le soupçonnions de longue date.