Cours n° 22, 12 avril 2012

Jean-François Perrot

Analyse ascendante


  1. Algorithme à pile shift-reduce
    1. L'algorithme d'analyse procède par une suite d'actions de deux sortes
    2. Idée de réduction / action
    3. Application n°1 : traduction en postfixée
    4. Application n° 2 : calcul de la profondeur de l'arbre
    5. Application n° 3 : évaluation d'une exp. compl. parenthésée
    6. Application n° 4 : Construction d'un arbre syntaxique
      1. La construction d'un arbre syntaxique est une forme d'évaluation "symbolique".
      2. Actions en vue de la construction de l'arbre syntaxique

  2. Réalisation élémentaire de l'analyse ascendante en C++
    1. Le cadre général
      1. Analyse conforme à la théorie
      2. Génération de l'arbre d'expression
    2. Notation complètement parenthésée
      1. Analyse conforme à la théorie
      2. Génération de l'arbre d'expression
    3. Notation polonaise préfixée
    4. Notation à précédences (2 niveaux)
      1. Principe
      2. Construction de l'arbre

Algorithme à pile shift-reduce

  1. L'algorithme d'analyse procède par une suite d'actions de deux sortes

     "shift" (empiler un lexème)
     "reduce" (trouver une partie droite de règle  en sommet de pile et la réduire =  la remplacer par le non-terminal correspondant)

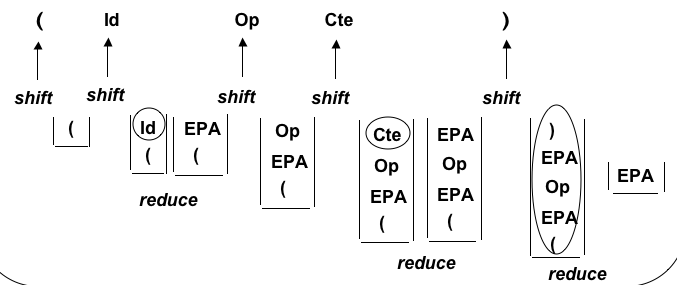
    Shift-Red


    Mouvements de la pile

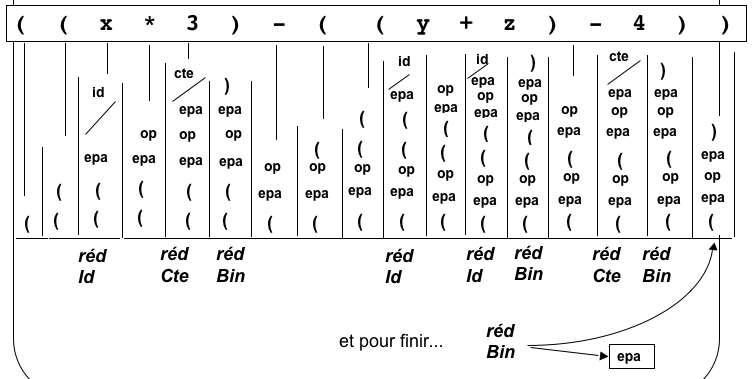
    Shift-Red - 2

  2. Idée de réduction / action


    On considère la séquence des réductions au cours du déroulement de l'algorithme shift-reduce.
    À chaque réduction on associe une action (dans le contexte où la réduction a lieu),
    et on s'intéresse au résultat produit par la séquence d'actions parallèle à la séquence des réductions.


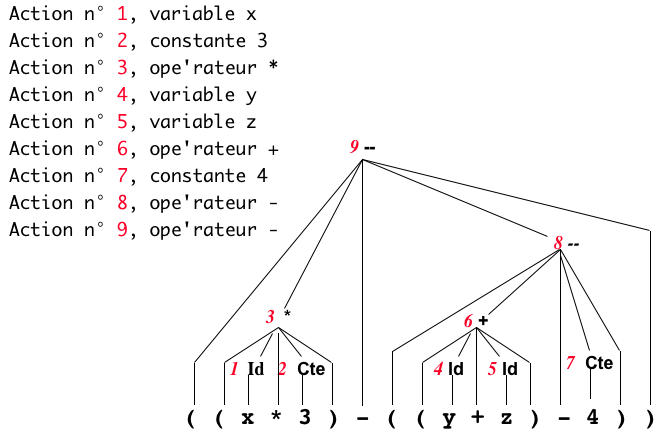
    Shift-Red - 3

  3. Application n°1 : traduction en postfixée


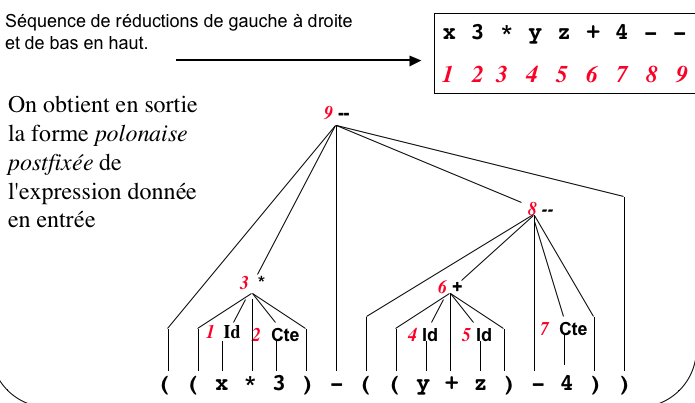
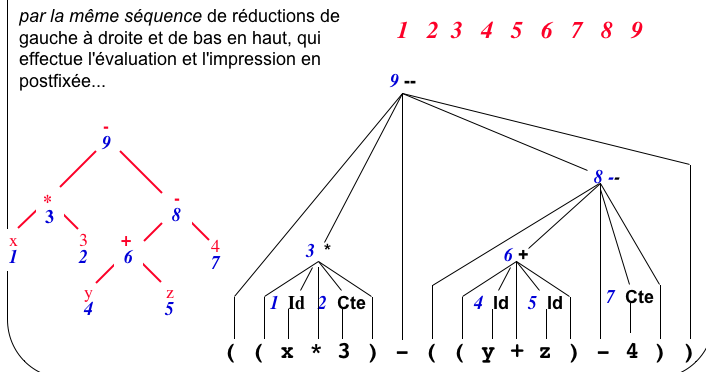
    Que faut-il faire pour que la séquence d'actions pilotée par le processus shift/reduce effectue la traduction en notation polonaise postfixée ?
    et ça marche !
    Question : peut-on traduire de la même manière en préfixée ?   NON !!!


    Shift-Red - 4




  4. Application n° 2 : calcul de la profondeur de l'arbre

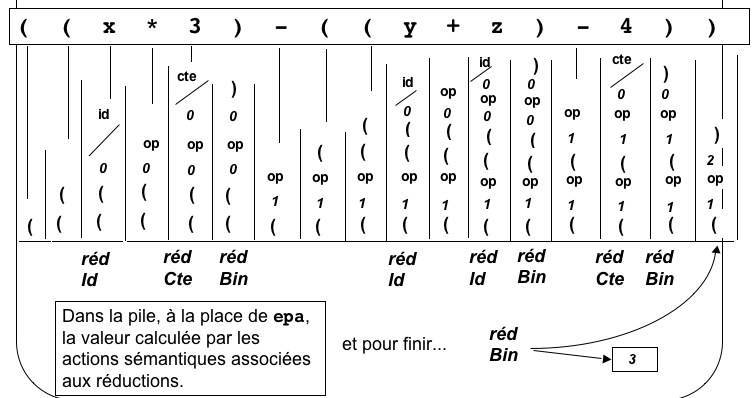
    Réductions / actions utilisant la pile
    À la fin du calcul, la profondeur de l'arbre tout entier est seule dans la pile.

    Shift-Red - 5

  5. Application n° 3 : évaluation d'une exp. compl. parenthésée

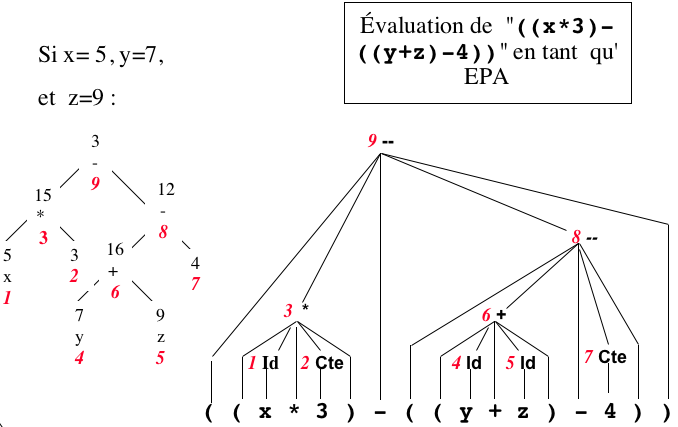
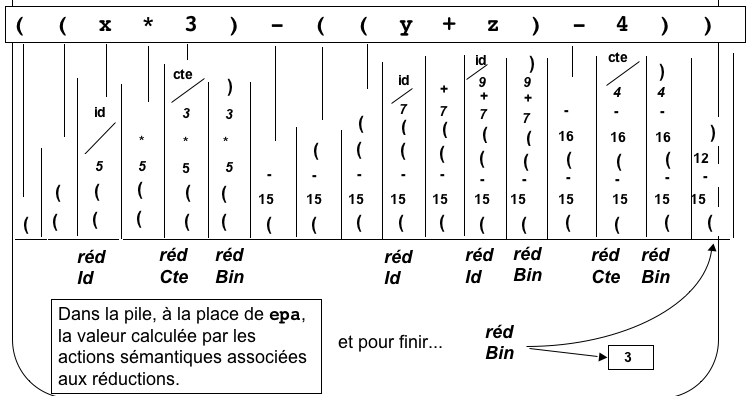
    Processus d'évaluation par réductions / actions

    À la fin du calcul, la valeur de l'arbre tout entier est seule dans la pile.

    Shift-Rred - 6

    Shift-Red - 7

  6. Application n° 4 : Construction d'un arbre syntaxique

    À la fin du calcul, l'arbre tout entier est seul dans la pile.


    Shift-Red - 8


Réalisation élémentaire de l'analyse ascendante en C++

  1. Le cadre général

    Tous les analyseurs que nous allons voir ont exactement la même structure.
    Nous nous tenons à une programmation qui reflète fidèlement le discours théorique.

    La classe pile que nous employons est la même que celle que nous avons mise en œuvre dans l'analyse descendante.

  2. Notation complètement parenthésée

    À comparer avec l'analyseur descendant pour la même grammaire

    Grammaire : la même que pour l'analyse descendante.
    1. S -> (S O S)
    2. S -> v
    3. S-> i
    4. O -> +
    5. O -> *

    Les symboles dans la pile sont ceux de la grammaire.
    La stratégie shift/reduce est limpide : la donnée du symbole en sommet de pile suffit
    Notez que shift comporte l'incrémentation de l'indice i, essentielle pour assurer la terminaison de la boucle while !
  3. Exercice : traiter de même la notation polonaise postfixée.

  4. Notation polonaise préfixée

    À comparer avec l'analyseur descendant pour la même grammaire.

    On doit distinguer deux états pour le non-terminal S

    Moyennant quoi nous sommes ramenés à la même situation que pour la grammaire CP
    à savoir que la donnée du symbole en sommet de pile suffit

    fichier apref1.cpp
            switch( sp ){
                case '+' :
                case '*' :
                case 'S' : { // shift
                    p->push(carlu);
                    i++;
                    break;
                } // case '+' '*' 'S'

                   case 'x' :
                   case 'y' :
                case 'z' :
                case '1' :        
                case '2' :                
                case '3' : { // reduce S -> term
                    p->pop();
                        if( p->top() == 'S' ){
                        p->push('T');
                    }else{
                        p->push('S');
                    }
                    break;
                }
                case 'T' : { // reduce S -> opSS
                    p->pop(); // de 'T'
                    if( p->top() != 'S' ){
                        cout << "Erreur dans la pile 'T' : " << p->top() << endl;
                        return 1;
                    }
                    p->pop(); // de 'S'
                    if( p->top() != '+' && p->top() != '*' ){
                         cout << "Erreur dans la pile 'S' : " << p->top() << endl;
                         return 1;
                    }
                    p->pop(); // de l'opérateur

                    if( p->top() == 'S' ){
                        p->push('T');
                    }else{
                        p->push('S');
                    }
                    break;
                } // case 'T'

                default : { cout << "Erreur symbole inconnu : " << sp << endl;
                            return 1;
                          }
            } // switch( p->top() )
        }// while
    Exécution :
    jfp% ./a.out
    *+xy*+x*y+z2+y3
    + -- *
    x -- + *
    y -- x + *
    y -- S + *
    * -- y S + *
    * -- T S + *
    * -- S *
    + -- * S *
    x -- + * S *
    * -- x + * S *
    * -- S + * S *
    y -- * S + * S *
    + -- y * S + * S *
    + -- S * S + * S *
    z -- + S * S + * S *
    2 -- z + S * S + * S *
    2 -- S + S * S + * S *
    + -- 2 S + S * S + * S *
    + -- T S + S * S + * S *
    + -- T S * S + * S *
    + -- T S + * S *
    + -- S * S *
    y -- + S * S *
    3 -- y + S * S *
    3 -- S + S * S *
    $ -- 3 S + S * S *
    $ -- T S + S * S *
    $ -- T S * S *
    $ -- T S *
    $ -- S
    OK

    La construction de l'arbre d'expression vous est proposée en exercice.

  5. Notation à précédences ( 2 niveaux)

    Grammaire :
    1. E -> E+T
    2. E -> T  
    3. T -> T*F
    4. T -> F 
    5. F -> v
    6. F -> i 
    7. F -> (E)

    1. Principe
      Cette fois, la stratégie shift/reduce est plus compliquée.

      • D'une part il nous faut distinguer deux états pour T et pour F (idée que nous avons déjà vue pour la polonaise préfixée) :
        • lorsque T se trouve empilé au-dessus de l'opérateur '+', il doit déclencher la réduction E -> E+T
          sinon il déclenche la réduction E -> T ;
        • lorsque F se trouve empilé au-dessus de l'opérateur '*', il doit déclencher la réduction T -> T*F
          sinon il déclenche la réduction T -> F .
        Nous écrirons donc 'D' pour 'T' au-dessus de '+', et ''G' pour 'F' au-dessus de '*'.

      • D'autre part, T (ou D) en sommet de pile provoque tantôt une réduction, tantôt un shift :
        • lorsque le prochain caractère à traiter est l'opérateur '*', c'est shift,
          car cet opérateur ne peut être là que par application de la règle T -> T*F, il faut donc continuer à lire !
        • dans tous les autres cas, reduce,
          la règle à réduire étant univoquement déterminée gâce à la distinction entre T et D.

      fichier aprec2.cpp
              switch( sp ){
                  case '(' :
                  case '+' :
                  case '*' :
                  case 'E' : { // shift dans tous les cas
                      p->push(carlu);
                      i++;
                      break;
                  } // case 'S' '+' '*'
                 
                  case 'T' : { // shift ou reduce selon carlu
                      if( carlu == '*' ){ // shift
                          p->push(carlu);
                          i++;
                      }else{ // reduce E -> T
                          p->pop(); // de 'T'
                          p->push('E');
                      }
                      break;
                  }
                  case 'D' : { // shift ou reduce selon carlu   
                      if( carlu == '*' ){ // shift
                          p->push(carlu);
                          i++;
                      }else{ // reduce E -> E+T
                          p->pop(); // de 'T'
                          if( p->top() != '+' ){
                              cout << "Erreur dans la pile 'D' : " << p->top() << endl;
                              return 1;
                          }
                          p->pop(); // de '+'
                          if( p->top() != 'E' ){
                              cout << "Erreur dans la pile '+' : " << p->top() << endl;
                              return 1;
                          }
                          // on laisse E en place
                      }
                      break;
                  } // case 'D'
                     
                  case 'F' : { // reduce T -> F
                      p->pop();
                      if( p->empty() || p->top() == '(' ){
                          p->push('T');
                      }else{ // '+'
                          p->push('D');
                      }
                      break;
                  }// case 'F'
                     
                  case 'G' : { // reduce T -> T*F
                      p->pop(); // de 'G'
                      if( p->top() != '*' ){
                          cout << "Erreur dans la pile 'V' : " << p->top() << endl;
                          return 1;
                      }
                      p->pop(); // de '*'
                      if( p->top() != 'T' && p->top() != 'D'){
                          cout << "Erreur dans la pile '*' : " << p->top() << endl;
                          return 1;
                      }
                      // on laisse T en place
                      break;
                  } //case 'G'
                 
                  case 'x' :
                  case 'y' :
                  case 'z' :
                  case '1' :        
                  case '2' :                
                  case '3' : { // reduce F -> term
                      p->pop();
                      if( p->empty() || p->top() == '(' || p->top() == '+' ){
                          p->push('F');
                      }else{ // '*'
                          p->push('G');
                      }
                      break;
                  }
                  case ')' : { // reduce F -> (E)
                      p->pop(); // de ')'
                      if( p->top() != 'E' ){
                          cout << "Erreur dans la pile '(' : " << p->top() << endl;
                          return 1;
                      }
                      p->pop(); // de 'E'
                      if( p->top() != '(' ){
                           cout << "Erreur dans la pile 'E' : " << p->top() << endl;
                           return 1;
                      }
                      p->pop(); // de ')'
                      if( p->empty() || p->top() == '(' || p->top() == '+' ){
                          p->push('F');
                      }else{ // '*'
                          p->push('G');
                      }
                      break;
                  } // case ')'

                  default : { cout << "Erreur symbole inconnu : " << sp << endl;
                              return 1;
                            }

              } // switch( p->top() )
      Exécution
      x+y*((z+3+x*y)+z)*2*z
      + -- x
      + -- F
      + -- T
      + -- E
      y -- + E
      * -- y + E
      * -- F + E
      * -- D + E
      ( -- * D + E
      ( -- ( * D + E
      z -- ( ( * D + E
      + -- z ( ( * D + E
      + -- F ( ( * D + E
      + -- T ( ( * D + E
      + -- E ( ( * D + E
      3 -- + E ( ( * D + E
      + -- 3 + E ( ( * D + E
      + -- F + E ( ( * D + E
      + -- D + E ( ( * D + E
      + -- E ( ( * D + E
      x -- + E ( ( * D + E
      * -- x + E ( ( * D + E
      * -- F + E ( ( * D + E
      * -- D + E ( ( * D + E
      y -- * D + E ( ( * D + E
      ) -- y * D + E ( ( * D + E
      ) -- G * D + E ( ( * D + E
      ) -- D + E ( ( * D + E
      ) -- E ( ( * D + E
      + -- ) E ( ( * D + E
      + -- F ( * D + E
      + -- T ( * D + E
      + -- E ( * D + E
      z -- + E ( * D + E
      ) -- z + E ( * D + E
      ) -- F + E ( * D + E
      ) -- D + E ( * D + E
      ) -- E ( * D + E
      * -- ) E ( * D + E
      * -- G * D + E
      * -- D + E
      2 -- * D + E
      * -- 2 * D + E
      * -- G * D + E
      * -- D + E
      z -- * D + E
      $ -- z * D + E
      $ -- G * D + E
      $ -- D + E
      $ -- E
      OK
    2. Construction de l'arbre d'expression
      Elle présente l'intérêt d'une simplification notable par rapport à l'arbre de dérivation,
      comme on l'a vu abondamment dans les cours précédents.
      Cette simplification se traduit tout bonnement par des réductions dans la pile qui ne produisent rien
      dans la construction de l'arbre : les règles E -> T,  T -> F,  F -> (E).

      Cette circonstance agréable est due à la compatibilité entre le parcours ascendant
      et la construction vue comme une évaluation symbolique.

      Voici la chose (fichier aprec2Arb.cpp) :
              switch( sp ){
                  case '(' :
                  case '+' :
                  case '*' :
                  case 'E' : { // shift dans tous les cas
                      if( carlu != '$' ){
                          p->push(carlu);
                      }
                      i++;
                      break;
                  } // case '(' 'E' '+' '*'
                 
                  case 'T' : { // shift ou reduce selon carlu
                      if( carlu == '*' ){ // shift
                          p->push(carlu);
                          i++;
                      }else{ // reduce E -> T       : on ne construit rien
                          p->pop(); // de 'T'
                          p->push('E');
                      }
                      break;
                  }
                  case 'D' : { // shift ou reduce selon carlu   
                      if( carlu == '*' ){ // shift
                          p->push(carlu);
                          i++;
                      }else{ // reduce E -> E+T : on construit
                          p->pop(); // de 'T'
                          arbd = pA->top();
                          pA->pop();
                         
                          if( p->top() != '+' ){
                              cout << "Erreur dans la pile 'D' : " << p->top() << endl;
                              return 1;
                          }
                          p->pop(); // de '+'
                          if( p->top() != 'E' ){
                              cout << "Erreur dans la pile '+' : " << p->top() << endl;
                              return 1;
                          }
                          // on laisse E en place
                          arbg = pA->top();
                          pA->pop();
                         
                          pA->push(new ArbExp('+', arbg, arbd));
                      }
                      break;
                  } // case 'D'
                     
                  case 'F' : { // reduce T -> F       : on ne construit rien
                      p->pop();
                      if( p->empty() || p->top() == '(' ){
                          p->push('T');
                      }else{ // '+'
                          p->push('D');
                      }
                      break;
                  }// case 'F'
                     
                  case 'G' : { // reduce T -> T*F : on construit
                      p->pop(); // de 'G'
                      arbd = pA->top();
                      pA->pop();
                     
                      if( p->top() != '*' ){
                          cout << "Erreur dans la pile 'V' : " << p->top() << endl;
                          return 1;
                      }
                      p->pop(); // de '*'
                      if( p->top() != 'T' && p->top() != 'D'){
                          cout << "Erreur dans la pile '*' : " << p->top() << endl;
                          return 1;
                      }
                      // on laisse T en place
                      arbg = pA->top();
                      pA->pop();
                         
                      pA->push(new ArbExp('*', arbg, arbd));
                      break;
                  } //case 'G'
                 
                  case 'x' :
                  case 'y' :
                  case 'z' :
                  case '1' :        
                  case '2' :                
                  case '3' : { // reduce F -> term
                      p->pop();
                      if( p->empty() || p->top() == '(' || p->top() == '+' ){
                          p->push('F');
                      }else{ // '*'
                          p->push('G');
                      }
                      pA->push(new ArbExp(sp));
                      break;
                  }
                  case ')' : { // reduce F -> (E) : on ne construit rien
                      p->pop(); // de ')'
                      if( p->top() != 'E' ){
                          cout << "Erreur dans la pile '(' : " << p->top() << endl;
                          return 1;
                      }
                      p->pop(); // de 'E'
                      if( p->top() != '(' ){
                           cout << "Erreur dans la pile 'E' : " << p->top() << endl;
                           return 1;
                      }
                      p->pop(); // de ')'
                      if( p->empty() || p->top() == '(' || p->top() == '+' ){
                          p->push('F');
                      }else{ // '*'
                          p->push('G');
                      }
                      break;
                  } // case ')'
                 
                  default : { cout << "Erreur symbole inconnu : " << sp << endl;
                              return 1;
                            }

              } // switch( p->top() )
      Exécution :
      x+y*((z+3+x*y)+z)*2*z
       
      mêmes mouvements de pile....
      et
      +x***y+++z3*xyz2z
      xyz3+xy*+z+*2*z*+
      OK