Arbre de dérivation
-
Idée
La propriété fondamentale des grammaires CF est que
les dérivations qui conduisent de l'axiome à un mot terminal peuvent se regrouper en arbres,
appelés arbres de dérivation.
Chaque règle de grammaire peut être vue comme un nœud étiqueté par le non-terminal de la règle
dont les fils sont étiquetés par les lettres du membre droit.
Par exemple, pour la grammaire que nous avons proposée plus haut pour les systèmes de parenthèses :

Une dérivation peut alors se représenter de manière naturelle en "accrochant les nœuds".
Exemple
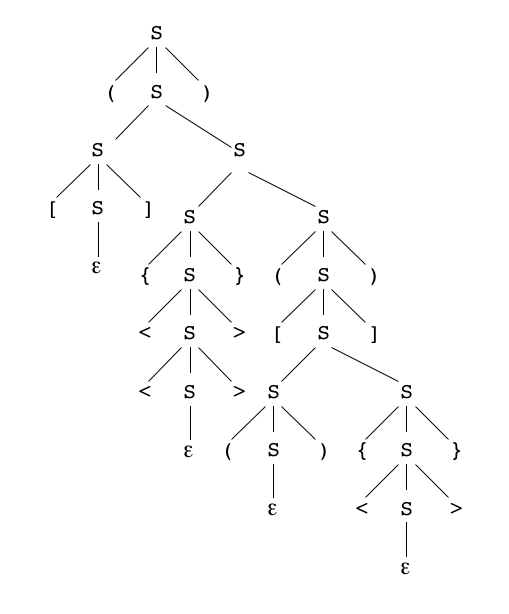
Voici un arbre de dérivation du mot bien parenthésé "([]{<<>>}([(){<>}]))" dans la grammaire ci-dessus :
S
3
( S )
1
( S S )
4 1
( [S] S S )
2 5 1
( [] {S} (S) )
6 4
( [] {<S>} ([S]) )
6 1
( [] {<<S>>} ([S S]) )
2 3 4
( [] {<<>>} ([(S){S}]) )
2 6
( [] {<<>>} ([(){<S>}]) )
2
( [] {<<>>} ([(){<>}]) )
-
Dérivation droite, dérivation gauche
Comme on le voit dès notre premier exemple, à chaque étape d'une chaîne de réécritures
on a en général le choix entre plusieurs occurrences de symboles non-terminaux à réécrire,
et ces occurrences sont ordonnées de la gauche vers la droite.
En choisissant de réécrire systématiquement le non-terminal le plus à gauche, on obtient une chaîne de réécritures
qui correspond au parcours de l'arbre de dérivation "en profondeur d'abord et de gauche à droite" :
pour notre exemple, c'est celle que nous avons donnée ci-dessus.
Une telle dérivation est appelée "dérivation gauche" (en anglais leftmost derivation).
On peut opérer de même à droite (rightmost derivation).
Je ne dis pas que toutes les dérivations peuvent être représentées par un seul arbre,
en raison du danger d'ambiguïté de la grammaire (voir plus loin),
mais du moins peut-on regrouper en un seul arbre les dérivations "apparentées". -
Grammaires CF vues comme des systèmes formels - l'arbre de dérivation comme arbre de preuve
-
Chaque règle de grammaire peut être vue comme une règle de déduction (en logique)
Chaque non-terminal s'interprète comme un prédicat dénotant l'appartenance de son argument (une chaîne terminale)
à une certaine catégorie grammaticale.
La partie droite de la règle de grammaire = prémisses de la règle de déduction.
Le non-terminal en partie gauche = sa conclusion
Exemple : les trois règles de réécriture de la grammaire suivante
(EPA= Expression complètement PArenthésée)
EPA -> IdEPA -> CteEPA -> '('EPA Op EPA')'

-
L'analyse syntaxique apparaît alors comme une démonstration, donnant naissance à un arbre de preuve ...
Exemple de preuve dans le système ci-dessus : par application répétée des 3 règles on prouve que l'expression donnée
( ( x * 3 ) - ( ( y + z ) - 4 ) )
est bien conforme à la grammaire, en partant de la "constatation" des caractères composant la chaîne lue.
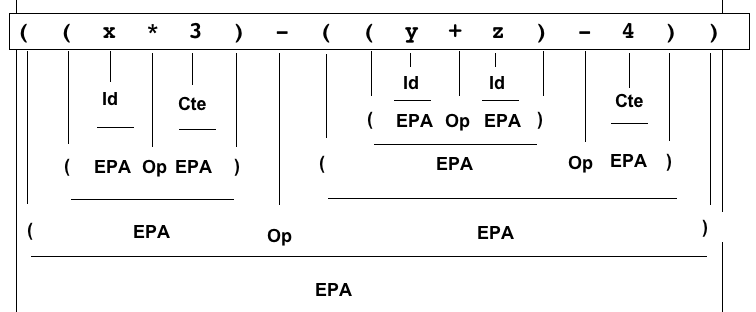
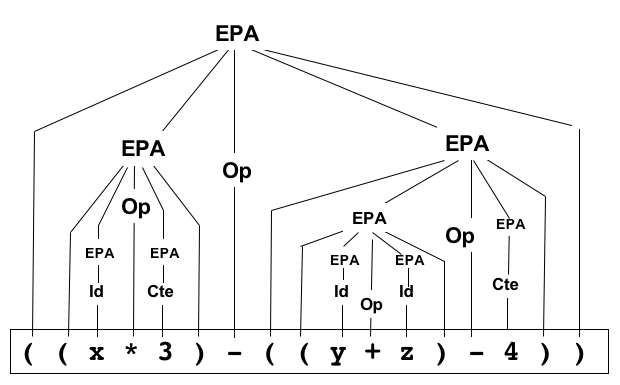
L'arbre de dérivation n'est qu'une autre manière de représenter l'arbre de preuve...
-
-
Interprétations
-
Interprétation de l'arbre de dérivation
On admettra que l'arbre de dérivation définit la structure syntaxique du mot engendré,
indépendamment de l'ordre dans lequel on a effectué les réécritures.
L'intérêt de cette notion est qu'elle sert de base à de multiples interprétations, dans le but d'attribuer
une signification au mot ainsi structuré.
Dans notre exemple parenthésé, une des significations possibles du mot est l'arbre que représente ce système de parenthèses
conformément à Systèmes de parenthèses et structures arborescentes.
Nous chercherons donc à interpréter l'arbre de dérivation dans ce sens (en assumant le jeu de mots) :
en termes opérationnels, comment construire "l'arbre du mot" à partir de l'arbre de dérivation ?
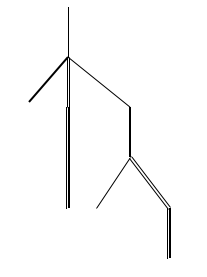
Les quatre sortes de traits dans l'arbre
symbolisent les quatre sortes de parenthèses dans le langage.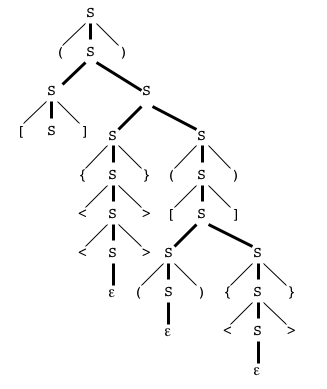
Comme on le devine avec cette image, la chose est possible, mais compliquée (contraction de certains sommets, ablation de feuilles,...).
En fait le problème se pose en des termes légèrement différents :
le but de l'analyse grammaticale étant de faire apparaître la signification, la structure syntaxique n'est pas un but mais un moyen.
On cherchera donc à construire l'arbre du mot au cours du processus d'analyse, qui consiste en un parcours de l'arbre de dérivation.
Et dès lors les choses seront beaucoup plus faciles !
-
La syntaxe comme base de la sémantique
En général, la signification attachée à un mot n'est pas un arbre en tant que tel, mais bien les différentes opérations
qu'on peut effectuer sur lui : l'arbre est vu comme un support pour d'autres élaborations.
L'exemple classique est celui des expressions arithmétiques
(au sens des langages de programmation : les mathématiciens diraient plutôt expressions algébriques).
Grammaire :
nous nous autorisons la licence de désigner parv(symbole terminal) une variable générique, qui pourra êtrex,y,z, etc,
et pari(autre symbole terminal) un entier générique qui pourra être... n'importe quel entier !
Les autres symboles terminaux sont les opérateurs arithmétiques+et*. Exemple : "x + y + z * 2"
S -> S+SS -> S*SS -> vS -> i
La grammaire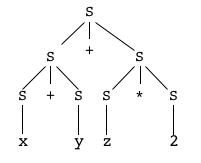
L'arbre de dérivation du mot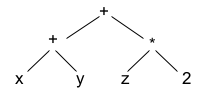
L'arbre de l'expression
(arbre syntaxique)
Ce que nous appelon l'arbre de l'expression sera ensuite évalué (dans un environnement où les trois variables trouveront leurs valeurs),
imprimé en diverses notations, voire traduit en une séquence d'instructions en assembleur...
Ce sont ces opérations qui définissent véritablement la sémantique du mot en question : par rapport à elles, l'arbre de l'expression
relève encore de la syntaxe, mais de la syntaxe abstraite.
C'est pourquoi il est généralement appelé l'arbre syntaxique (syntax tree) - proche mais bien différent de l'arbre de dérivation !
-
-
Ambiguïté
-
Ambiguïté de la grammaire
Il saute aux yeux que l'arbre de dérivation que nous avons proposé ci-dessus pour le mot "x + y + z * 2"
n'est pas unique ! C'est celui qui correspond à notre lecture du mot, mais la grammaire produit aussi les deux suivants :
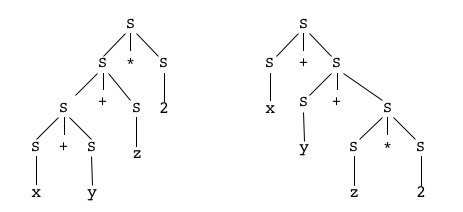
qui donnent tout aussi légitimement deux autres arbres d'expressions,
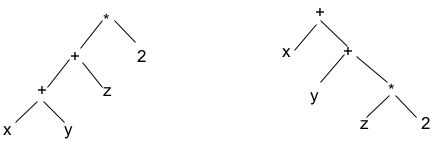
dont on est bien certain qu'ils n'auront pas la même signification !
On dit que le mot considéré est ambigu - puisqu'il peut recevoir plusieurs significations différentes -
et que la grammaire elle-même est ambiguë [Wikipedia]
-
Rectification : grammaire non-ambiguë
Dans le cas de notre exemple, il est assez facile de construire une grammaire non-ambiguë pour le langage,
c'est à-dire qui impose un seul arbre de dérivation (nous reviendrons plus tard sur le procédé employé ici).
S -> S+T
S -> TT -> T*UT -> UU -> vU -> i
La grammaire
non-ambiguë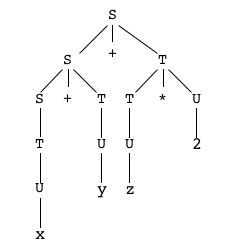
L'arbre de dérivation du mot
"x + y + z * 2"
L'arbre de l'expression
(arbre syntaxique)
Mais cette "réparation" n'est pas toujours facile... elle est même parfois impossible !
-
Ambiguïté inhérente
On dit qu'un langage est inhéremment ambigu (anglais : inherently ambiguous) si toutes ses grammaires sont ambiguës.
L'exemple classique est L = {anbncmdm | n>0, m>1} ∪ {anbmcmdn | n>0, m>1}.
On montre que les mots de la forme apbpcpdp sont nécessairement engendrés deux fois.
Nous nous bornerons à illustrer la chose :
Grammaire :
S -> ABS -> CA -> aAbA -> abB -> cBdB -> cd
C -> aCdC -> aDd
D -> bDcD -> bc
Deux dérivations "à gauche" pour le motaabbccdd
S -> AB -> aAbB-> aabbB -> aabbcBd -> aabbccdd
S -> C -> aCd -> aaDdd -> aabDcdd -> aabbccdd
et les arbres de dérivation associés, aux structures bien différentes :
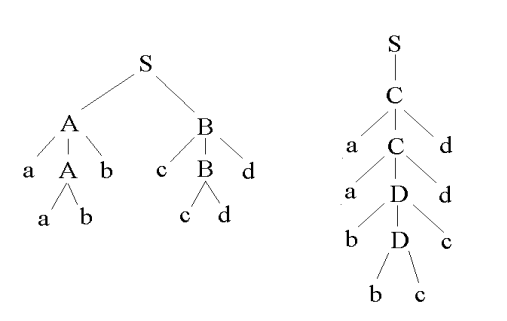
-
Non-déterminisme (de l'automate à pile) et ambiguïté inhérente (de la grammaire)
Si un langage CF est inhéremment ambigu, il ne peut pas être déterministe,
car à partir de l'automate déterministe on pourrait construire une grammaire non-ambiguë.
(Ce raisonnement intuitif peut être rendu rigoureux).
Mais l'exemple des palindromes montre que la réciproque n'est pas vraie :
le langage des palindromes est non-déterministe mais n'est nullement ambigu !
-
Résoudre l'ambiguïté dans les grammaires CF
-
Une source d'ambiguïté : les séquences
-
Exemple 1 : parenthèses
Revenons à notre 1er exemple, la grammaire pour le langage des systèmes de parenthèses :
elle énonce qu'un système de parenthèses est formé d'un suite finie de systèmes indécomposables,
cette suite est produite par la règle 1, les règles 3 à 6 se chargeant d'engendrer des systèmes indécomposables.
Or, cette règle 1 est ambiguë !
Soit le système parenthésé "()()()" formé de 3 systèmes indécomposables :
on peut produire cette séquence de deux manières avec deux application de la règle 1,
selon que la seconde application de ladite règle se fait "à gauche" ou "à droite", d'où deux arbres de dérivation différents :
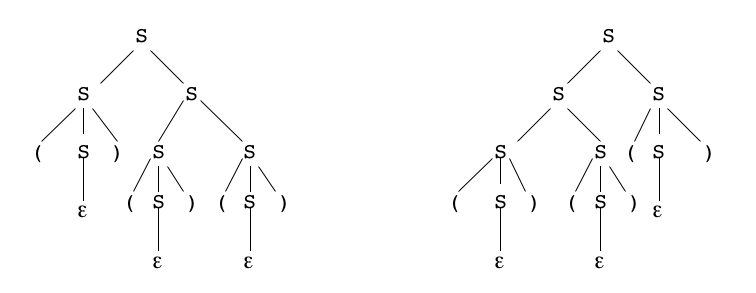
À l'égard de l'interprétation de ces mots comme représentant des arbres, cette différence est sans conséquence,
dans les deux cas on trouve le même petit arbre
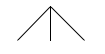
Mais on pourrait viser une interprétation où la différence serait sensible !
La solution standard est d'éviter la règle 1, en précisant à chaque règle la nature du premier système indécomposable,
c'est-à-dire :
S -> εS -> (S)SS -> [S]SS -> {S}SS -> <S>S
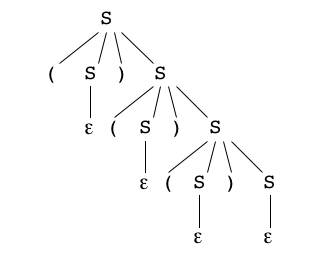
-
Exemple 2 : Expressions arithmétiques
Il faut bien voir que l'ambiguïté de cette grammaire est de la même nature que celle de la règle 1 des systèmes parenthésés.
Dans les deux cas il s'agit d'engendrer une séquence uniforme, en faisant abstraction du sens de lecture de cette séquence
(de gauche à droite ou de droite à gauche).
C'est là que se trouve l'erreur : dans la plupart des cas, une séquence se lit d'une certaine manière, qui lève l'ambiguïté.
Comme le domaine d'application privilégié de cette observation est la syntaxe des expressions arithmétiques,
où il est souvent question d'opérateurs associatifs, on parle d'association à gauche ou à droite.
La rectification que nous avons apportée à cette grammaire relève du choix d'association à gauche.
-
-
Association à gauche ou à droite
-
à gauche :
La règle d'association à gauche impose de lire une somme de plusieurs termes "a+b+c+d"
comme une série de d'additions de deux termes parenthésée à gauche "(((a+b)+c)+d)",
La soustraction est traitée sur le même pied que l'addition (cf. la notion de somme algébrique),
ce qui montre que l'association à gauche n'a rien à voir avec la propriété d'associativité de l'addition,
puisque la soustraction n'est pas associative.
Ainsi, une soustraction de plusieurs termes "a-b-c-d" se lit "(((a-b)-c)-d)".
Le tout s'exprime par la proto-grammaire :
Somme = Somme [+|-] Terme | Terme ;
[et non"Somme : Terme[+|-]Somme | Terme ;"qui aboutirait à la décomposition à droite "(a-(b-(c-d)))" ].
De même, un produit de plusieurs facteurs "a*b*c*d"
parenthésée à gauche "(((a*b)*c)*d)",
Il en va de même pour une suite de quotients "a/b/c/d" -> "(((a/b)/c)/d)" et non "(a/(b/(c/d)))" !
Le tout est spécifié par
Produit : Produit [*|/] Facteur | Facteur ;
Telle est l'intention exprimée par la grammaire non-ambiguë vue ci-dessus.
Bien noter que le langage qu'elle décrit ne comporte point de parenthèses,
ce qui ne permet pas de produire des arbres d'expressions où une somme serait facteur d'un produit...
-
à droite :
Il se trouve plusieurs classes de séquences qui se lisent au contraire comme des listes :
d'abord le premier élément, puis le reste, et dans le reste d'abord le premier élément, puis le reste du reste, etc.
jusqu'à arriver à un reste vide.
Cest le cas notamment, en programmation, des séquences d'instructions :
une suite de 3 affectations, commep = p+2; s = s+p; n := n-1;
s'exécute comme "p = p+2; {s = s+p; n := n-1;}".
On écrit donc une grammaire avec association à droite :
SEQINST -> INST
SEQINST -> INST SEQINST
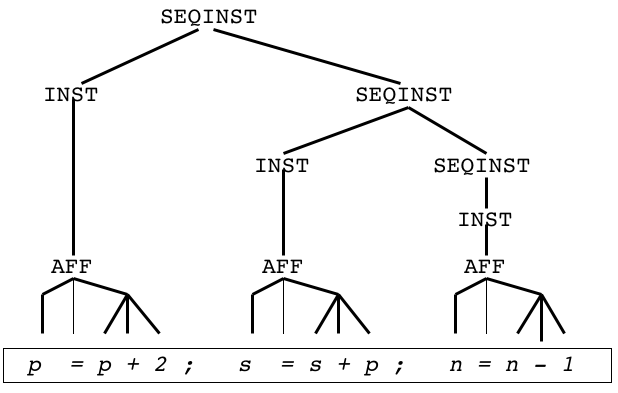
Arbre de dérivation
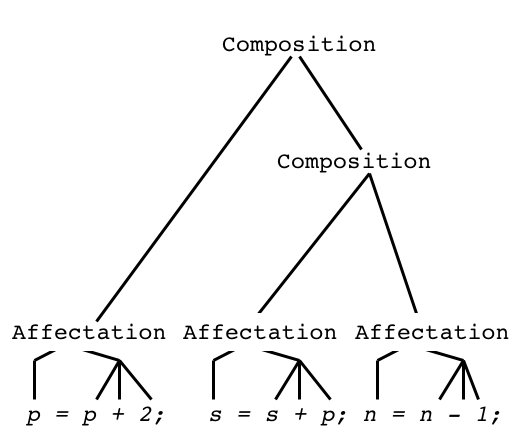
Arbre syntaxique
De même pour une suite de déclarations, etc.
-
Grammaires classiques pour les expressions arithmétiques
La grammaire des expressions a fait l'objet dans le passé d'études très approfondies.
C'est que les mathématiciens avaient en la matière des habitudes séculaires, auxquelles ont dû se plier les concepteurs de langages de programmation,
contrairement aux autres structures des langages pour lesquelles les programmeurs ont pu en faire à leur tête.
Il en résulte un certain nombre d'acquis techniques qu'il convient de bien comprendre car ils servent de modèles dans beaucoup de situations.
Nous nous limitons ici à des expressions à deux opérateurs binaires, l'addition et la multiplication (sauf dans notre dernier exemple).
Nous adoptons les mêmes conventions que précédemment pour les variables et les constantes.
-
Les notations polonaises
On les appelle ainsi car elles furent inventées en 1920 par le logicien polonais Jan Łukasiewicz,
qui de cette manière montra à ses collègues que les parenthèses dans les notations ne jouaient aucun rôle substantiel.
Elles se caractérisent en effet par l'absence de parenthèses, la position des opérateurs suffisant au codage,
à condition que leur "arité" (leur nombre d'arguments) soit fixe.
-
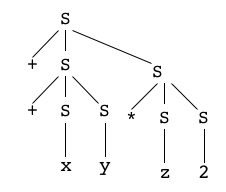
La notation polonaise préfixée
Comme son nom l'indique, l'opérateur est placé en tête, suivi de ses deux opérandes.
S -> +SSS -> *SSS -> vS -> i
++xy*z2

-
La notation polonaise postfixée
Comme son nom l'indique, l'opérateur est placé en queue, immédiatement précédé de ses deux opérandes.
Cette notation est particulièrement bien adaptée au calcul automatique de gauche à droite :
au fur et à mesure de la lecture, on évalue constantes et variables, on empile la valeur,
et quand on rencontre un opérateur on sait que ses deux arguments sont au sommet de la pile, il n'y a plus qu'à l'appliquer.
S -> SS+S -> SS*S -> vS -> i
xy+z2*+
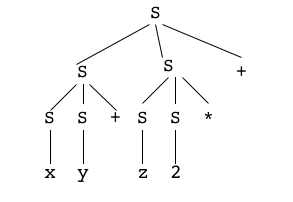

On note que le renversement d'une écriture postfixée donne une expression préfixée correcte, mais différente,
et réciproquement.
-
-
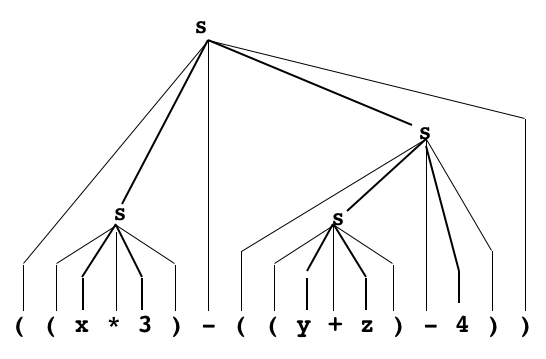
La notation complètement parenthésée
C'est la solution de base pour lever l'ambiguïté propre à la notation infixée des opérateurs binaires.
S -> (S+S)S -> (S*S)S -> vS -> i
((x*3)-((y+z)-4))
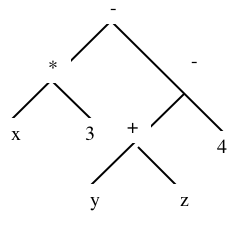
Comme on sait, l'emploi de parenthèses comme marqueurs syntaxiques est extrêmement répandu.
Les parenthèses prennent des formes diverses, notamment les balises de HTML et de XML, mais le principe demeure inchangé.
-
La notation traditionnelle à précédences (alias priorité des opérateurs)
-
Forme de base, avec deux niveaux de priorité
elle énonce que
- la multiplication a priorité sur l'addition,
c'est-à-dire que "
a+b*c" se lit "a+(b*c)" et non "(a+b)*c"
et plus généralement
les opérateurs multiplicatifs (multiplication et division) ont priorité sur les opérateurs additifs (addition et soustraction) ; - les deux classes d'opérateurs suivent la règle d'association à gauche (cf. ci-dessus)
- les parenthèses rompent la priorité.
comme un archaïsme (mot du vocabulaire diplomatique, relatif au protocole...).
EXPAR -> EXPAR + TERMEEXPAR -> TERMETERME -> TERME * FACTEURTERME -> FACTEURFACTEUR -> ( EXPAR )FACTEUR -> vFACTEUR -> i
x*3-(y+z-4)
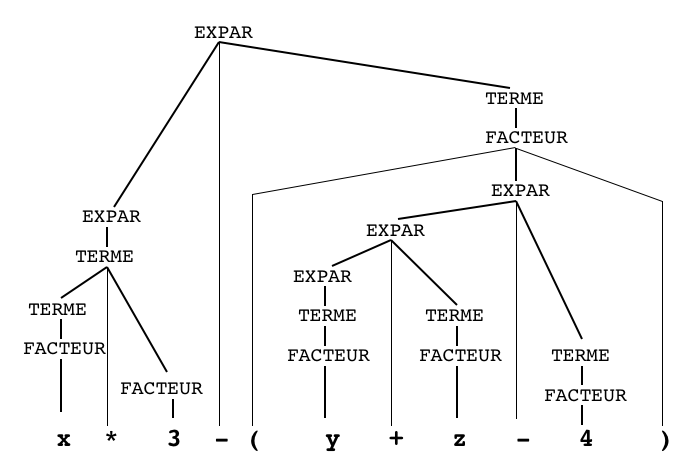

- la multiplication a priorité sur l'addition,
c'est-à-dire que "
-
Forme plus complète avec trois niveaux de priorité
On ajoute l'opérateur d'exponentiation, noté "^" : on écrit "x^2" pour "x2".
Cet opérateur a priorité sur les opérateurs multiplicatifs, et en outre il suit la règle d'association à droite (cf. ci-dessus).
En effet, "x^2^3" se lit "x^(2^3)" pour "x8" et non "(x^2)^3" pour "x6" qu'on écrirait de préférence "x^(2*3)".
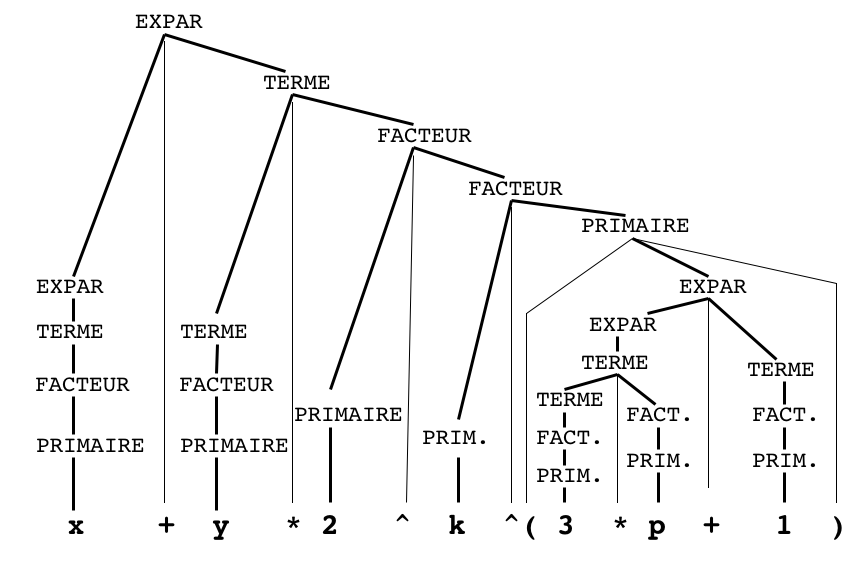
EXPAR -> EXPAR + TERMEEXPAR -> TERME
TERME -> TERME * FACTEURTERME -> FACTEUR
FACTEUR ->PRIMAIRE^FACTEURFACTEUR ->PRIMAIRE
PRIMAIRE -> ( EXPAR )PRIMAIRE-> vPRIMAIRE-> i
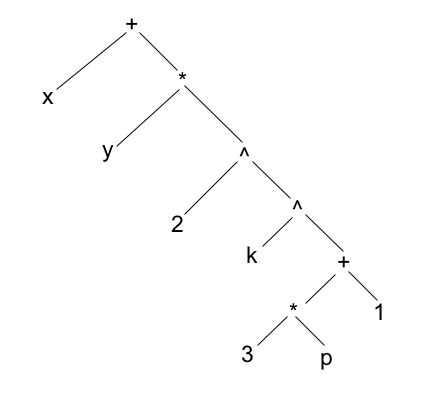
x+y*2^k^(3*p+1)
-