Cours n° 17, 8 mars 2012

Jean-François Perrot

Le formalisme des grammaires

1. Les grammaires comme systèmes de réécriture
   1. Définition
   2. Exemple
      1. Définition
      2. Montrons le processus
      3. Le problème des mots pour ce système est facile à résoudre
   3. Les grammaires comme cas particulier de systèmes de réécriture
   4. Grammaires et automates
      1. Problématique
      2. Machines de Turing
      3. Résultat
         
         
2. Grammaires context-sensitive
   1. Définitions
   2. Langage
   3. Grammaires non-contractantes
   4. Exemples de langages CS
      1. {aⁿbⁿcⁿdⁿ |  n>0}
      2. {ww | w ∈ {a, b}*}
      3. Exercices
   5. Automates linéairement bornés

Les grammaires comme systèmes de réécriture

1. Définition

   Voici les caractéristiques générales des systèmes de réécriture :
   
   
   • On part de l'ensemble des mots sur un alphabet (fini) X.
     Cet ensemble sera ici désigné par X*, comme dans les cours précédents (à partir du cours n° 3).
     L'opération de concaténation des mots va jouer un rôle essentiel.
     
     
   • On se donne une famille R de couples de mots
     (en termes mathématiques, R est une relation binaire sur X*) ;
     Ces couples de mots qui sont appelés règles de réécriture.
     On les note couramment avec une flèche : (a, b)∈ R s'écrira "a -> b", prononcé "a se réécrit en b".
     
     
   • On étend la relation R en deux étapes, de la manière suivante 
     
     
     1. étant donnés deux mots quelconques u, v∈X* et  un couple (a, b)∈ R,
        
        • on dit encore que le mot uav se réécrit en ubv [grâce à la règle (de réécriture) "a -> b"],
        • et on note également "uav -> ubv".
          
          
     2. on considère la fermeture transitive de cette relation :
        en utilisant au besoin plusieurs couples (a,b), (a',b'), (a",b")∈ R
        uav -> ubv = u'a'v' -> u'b'v' = u"a"v" -> u"b"v", etc.
        et on note uav ->* u"b"v".[ bien noter l'étoile dans ->* ]
        
     
     
   • On se pose la question "étant donnés deux mots p, q ∈ X*, peut-on décider si p ->* q ?
     Cette question est connue sous le nom de problème des mots pour le système considéré (en anglais word problem),
     et on démontre qu'il n'y a pas de solution générale au problème des mots :
     il n'existe pas d'algorithme qui prenne comme donnée la définition du système (ses règles de réécriture)
     et qui fournisse une solution du problème des mots pour ce système.
     
     Ce qu'on résume en disant que le problème des mots est indécidable.
     
     

2. Exemple

   • Définition

     X = { '(', ')', '[' , ']', '{' , '}' , '<' , '>'} l'ensemble des "parenthèses généralisées" (voir la section de cours sur les arbres),
     Nous notons 'ε' le mot vide.
     Les règles de réécriture sont
     
     1. () -> ε  
     2. [] -> ε 
     3. {} -> ε 
     4. <> -> ε  
     L'ensemble des mots qui peuvent se réécrire en ε est exactement l'ensemble des mots bien parenthésés.
     

   • Montrons le processus

     pour le mot "([]{<<>>}([(){<>}]))"
     en procédant de gauche à droite pour choisir quelle règle appliquer :
     
     ([]{<<>>}([(){<>}])) -2> ( {<<>>}([(){<>}]))
     -4> ({< >}([(){<>}])) -4> ({ }([(){<>}])) -3> ( ([(){<>}]))
     -1> (([ {<>}])) -4>  (([{ }])) -3>  (([ ])) -2> (( )) -1>  ( )  -1> ε
     
     On aurait pu procéder de droite à gauche, en obtenant une suite de réécritures différente
     mais conduisant au même résultat.
     Toutes les réécritures possibles se résument sous la forme de l'arbre ci-dessous :
     
     
     ([]{<<>>}([(){<>}]))
      2     4           1    4      
     (  {<  >}([  {  }]))
       4                3
     (  {    }([      ]))
 3             2
(        (        ))
                      1
     (                  )
     1
     ε
     
     
     

   • Le problème des mots pour ce système est facile à résoudre

     L'arbre ci-dessus se généralise à toutes les réécritures possibles à partir d'un mot quelconque,
     aboutissant à un mot qui ne contient plus aucun digramme dela forme "ouvrante -fermante".
     Étant donnés deux mots p, q ∈ X*, pour savoir si  p ->* q, il suffit de tracer l'arbre des réécritures
     à partir du mot p, et d'examiner si q apparaît à l'un de ses étages.
     
     La clé du succès est ici que chaque réécriture aboutisse à un mot réécrit plus court que le mot d'origine.
     C'est un système très particulier !
     

3. Les grammaires comme cas particulier de systèmes de réécriture

   Définition : une grammaire est
   
   
   • un système de réécriture dont l'alphabet est partagé en deux parties non vides :
     
     1. les symboles terminaux d'une part,
        
     2. les (symboles) non-terminaux d'autre part (aussi appelé symboles auxiliaires).
     
     
   • on choisit un symbole non-terminal appelé axiome, traditionnellement désigné par S (comme start symbol)
     (unique)
     
     
   • on s'intéresse à l'ensemble des mots w∈ X* tels que
     
     1. S ->* w (w peut être obtenu par réécriture à partir de l'axiome)
     2. et w ne contient aucun symbole non-terminal
        
        
     Cet ensemble de mots terminaux est appelé le langage engendré par la grammaire.
     
     
   • le problème des mots (ou du mot) pour une grammaire G est :
     étant donné un mot (terminal) w, décider s'il appartient ou non au langage engendré par G.
   
   L'originalité des grammaires parmi les systèmes de réécriture est cette nécessité de "chasser les non-terminaux"
   dans le processus de génération des mots du langage.
   
   Exemple : Grammaire G1
   (les non-terminaux sont en majuscules, les terminaux en minuscules)
   
   
   1. S -> aBSc
   2. S -> abc
   3. Ba -> aB
   4. Bb -> bb
   
   Essayons : S -> aBSc -> aBaBScc -> aBaBaBSccc -> et en général -> (aB)nScn par la règle 1.
   Pour chasser S il faut employer la règle 2 : -> (aB)nabccn
   Pour chasser tous les B, il faut les amener à des positions où ils n'ont que des b à leur droite,
   en les déplaçant grâce à la règle 3. On arrive ainsi à aanBnbccn , et par la règle 4 à aanbnbccn.
   On voit en outre que ce type de réécriture est le seul qui conduise à l'élimination complète des non-terminaux.
   Le langage engendré par cette grammaire est donc {anbncn | n >0}.
   
   

4. Grammaires et automates

   1. Problématique

      Toute la théorie des grammaires consiste à imposer diverses restrictions aux règles de réécriture
      et à étudier l'impact de ces restrictions sur les solutions possibles au problème des mots.
      Les solutions en question, qui sont des algorithmes, sont souvent décrites dans le format des automates
      (cf. cours n° 4),
      et on a coutume de mettre en rapport des classes de grammaires et des classe d'automates.
      
      Nous verrons prochainement quelles restrictions sont nécessaires pour obtenir les automates finis.
      Avant d'en arriver là, l'attention se porte sur la manière dont l'automate va gérer sa mémoire.
      Cette mémoire est vue comme une bande infinie sur laquelle l'automate lit et écrit des informations
      (des symboles comme ceux de l'alphabet), et le long de laquelle il peut déplacer sa tête de lecture-écriture,
      à l'image des bandes magnétiques qui étaient un composant essentiel des ordinateurs d'autrefois.
      

   2. Machines de Turing

      Sous sa forme la plus générale, on appelle un tel automate une machine de Turing
      (en hommage à Alan Turing, génial précurseur, qui inventa ce concept en 1936)
      
      
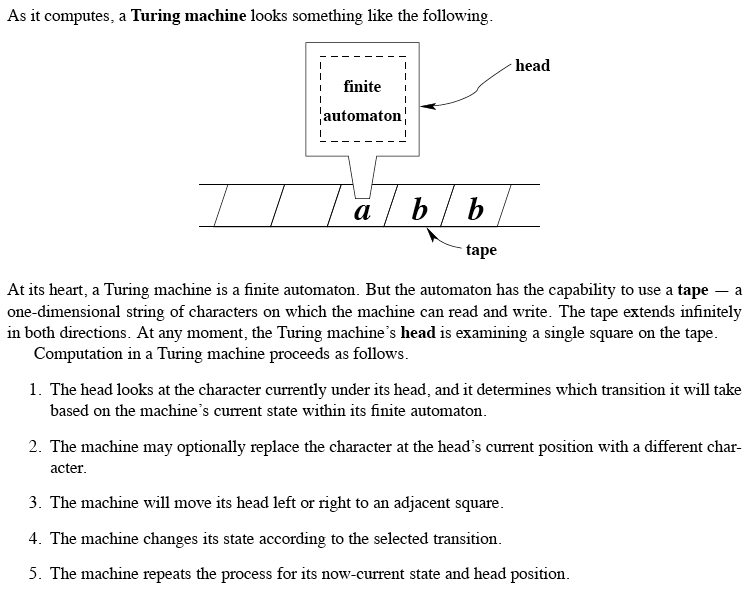
      source : http://ozark.hendrix.edu/~burch/socs/written/text/v1.pdf
      
      On a démontré que le modèle de la machine de Turing était une des formalisations de la notion de calculabilité :
      tout ce qui est calculable peut être calculé par une machine de Turing. [Thèse de Church]
      
      

   3. Résultat

      La classe d'automates associée à la classe des grammaires sans restriction sur leurs règles
      est celle des machines de Turing.
      En d'autres termes, pour décider si un mot appartient au langage engendré par une grammaire,
      il faut en général une machine de Turing.
      
      Nous allons à présent envisager plusieurs restrictions sur la forme des règles de réécriture,
      suivant la démarche dite de la hiérarchie de Chomsky.
      

Grammaires context-sensitive

1. Définitions

   La contrainte sur les règles d'un grammaire context-sensitive est la suivante :
   chaque règle est de la forme uAv -> uxv, où
   
   • u et v  sont des mots quelconques
   • x est un mot quelconque non-vide 
   • A  est un symbole non-terminal.
     
     
   La contrainte de non-viduité de x entraîne que
   le membre droit d'une règle est au moins aussi long que son membre gauche.
   
   L'appellation context-sensitive vient de ce que les mots u et v sont interprétés comme
   le contexte dans lequel le non-terminal A peut se réécrire en x.
   Nous verrons bientôt le modèle context-free où ce contexte ne joue aucun rôle.
   
   La grammaire G1 de l'exemple ci-dessus n'est pas context-sensitive, en raison de la règle n° 3
   Ba -> aB, qui n'est pas de la forme requise.
   Nous allons voir que ce défaut n'est pas essentiel.
   
   

2. Langage

   On appelle langage context-sensitive tout langage pour lequel il existe une grammaire CS qui l'engendre.
   
   Comme nous allons le voir abondamment, pour un langage donné il existe un grand nombre de grammaires
   qui l'engendrent - on dirait volontiers qu'il en existe une infinité !
   Deux grammaires seront donc dites équivalentes si elles engendrenr le même langage.
   
   Voici une grammaire G2 équivalente à G1, c'est-à-dire engendrant elle aussi {anbncn | n >0},
   et qui est bien CS, elle ! Ce qui démontre que ce langage est un lancage CS...
   
   
   1. S -> aSBC
   2. S -> aBC
   3. CB -> HB
   4. HB -> HC
   5. HC -> BC
   6. aB -> ab
   7. bB -> bb
   8. bC -> bc
   9. cC -> cc
   
   À titre d'exemple, voici une dérivation de "aaabbbccc" (n = 3).
   
   
   1. S  (départ)
   2. aSBC (1)
   3. aaSBCBC (1)
   4. aaaBCBCBC (2)
   5. aaaBHBCBC (3)
   6. aaaBHCCBC (4)
   7. aaaBBCCBC (5)
   8. aaaBBCHBC (3)
   9. aaaBBCHCC (4)
   10. aaaBBCBCC (5)
   11. aaaBBHBCC (3)
   12. aaaBBHCCC (4)
   13. aaaBBBCCC (5)
   14. aaabBBCCC (6)
   15. aaabbBCCC (7)
   16. aaabbbCCC (7)
   17. aaabbbcCC (8)
       
   18. aaabbbccC (9)
   19. aaabbbccc (9)
   
   En examinant cette réécriture, on voit que les trois règles CS n° 3, 4 et 5 n'ont pas d'autre but que de réaliser
   l'interversion CB ->* BC, par CB -3> HB -4> HC -5> BC.
   Mis à part cet aspect réglementaire, la stratégie de G2 est assez comparable à celle de G1.
   
   

3. Grammaires non-contractantes

   Une grammaire est non-contractante (en anglais non-contracting)
   si le membre droit de chaque règle est au moins aussi long que son membre gauche.
   Nous avons vu que toute grammaire CS est non-contractante,
   et l'exemple de G1 montre que la réciproque n'est pas vraie.
   
   Toutefois, on peut généraliser la démarche qui fait passer de G1 à G2 et montrer que
   pour toute grammaire non-contractante, il existe une grammaire CS équivalente,
   en ce sens qu'elle engendre le même langage.
   En d'autres termes, les grammaires non-contractantes engendrent exactement la classe des langages CS.
   
   On peut aller plus loin et montrer que toute grammaire non-contractante est équivalente à une
   grammaire en forme normale de Kuroda , où toutes les règles sont d'une des quatre formes :
   AB → CD
A → BC
A → B
A → a
   
   Les exemples de grammaires qui suivent seront donc donnés sous forme non-contractante.
   
   

4. Exemples de langages CS

   • {anbncndn | n>0}

     avec une stratégie assez différente de celle de G1 ou G2 pour {anbncn | n >0}.
     
     
     1. S → abcd
     2. S → aXbcd
     3. Xb → bX
     4. Xc → bYc
     5. Yc → cY
     6. Yd → Rcdd
     7. cR → Rc
     8. bR → Rb
     9. aR → aaX
     10. aR → aa
     
     
     
     Voyons la dérivation de "aaabbbcccddd" (n = 3) :
     
     
     1. S -2> aXbcd (parce qu'on ne veut pas se contenter de "abcd")
        
     2. -3> abXcd 
     3. -4> abbYcd
     4. -5> abbcYd
     5. -6> abbcRcdd
     6. -7> abbRccdd
     7. -8> abRbccdd
     8. -8> aRbbccdd
     9. -9> aaXbbccdd
     10. -3> aabXbccdd
     11. -3> aabbXccdd
     12. -4> aabbbYccdd
     13. -5> aabbbcYcdd
     14. -5> aabbbccYdd
     15. -6> aabbbccRcddd
     16. -7> aabbbcRccddd
     17. -7> aabbbRcccddd
     18. -8> aabbRbcccddd
     19. -8> aabRbbcccddd
     20. -8> aaRbbbcccddd
     21. -10> aaabbbcccddd
     
     
     On observe que
     
     • dans chaque mot de la chaîne sauf le dernier se trouve un seul non-terminal
     • à chaque étape une seule règle est applicable, à l'exception du pas initial et des étapes 8 et 21.
       
       
     Le pas intial a été commenté.
     
     L'autre choix se présente lorsque"aR" apparaît : soit on fait disparaître le non-terminal R par la règle 10
     (comme au pas 21), soit on relance le calcul par la règle 9, comme au pas 9.
     
     Le système fonctionne comme une navette sur un métier à tisser : l'unique non-terminal parcourt la chaîne
     de gauche à droite et de droite à gauche, en changeant de nom et en produisant au passage tantôt un b,
     tantôt un c, tantôt un d et enfin un a.
     On peut appliquer le même principe à plus de quatre lettres...
     
     

   • {ww | w ∈ {a, b}*}

     1. S -> ABC
     2. AB -> aAD
     3. AB -> bAE
     4. DC -> BaC
     5. EC -> BbC
     6. Da -> aD
     7. Db -> bD
     8. Ea -> aE
     9. Eb -> bE
     10. AB -> ε
     11. C -> ε
     12. aB -> Ba
     13. bB -> Bb
         
     
     Voyons une dérivation pour le mot "abbabb"
     
     1. S -1> ABC
     2. -2> aADC (on veut un mot qui commence par a, pas par b)
     3. -4> aABaC 
     4. -3> abAEaC (après le a on veut un b, pas un a)
     5. -8> abAaEC
     6. -5> abAaBbC 
     7. -12> abABabC 
     8. -3> abbAEabC (on veut encore un b,  pas un a)
     9. -8> abbAaEbC   
     10. -9> abbAabEC
     11. -5> abbAabBbC
     12. -13> abbAaBbbC
     13. -12> abbABabbC
     14. -10> abbabbC
     15. -11> abbabb
     
     De même que dans l'exemple précédent, la plupart du temps une seule règle est applicable.
     Le seul choix se trouve entre les règles 2 et 3, qui produisent l'une un a l'autre un b
     dans le premier mot. Ce choix permet donc de construire le mot w de manière arbitraire.
     La mécanique des non-terminaux B, D et E a pour rôle de construire lettre à lettre le même mot
     en seconde position.
     Dès qu'un a est produit à gauche (par la règle 2) le non-terminal D fait apparaître un a de l'autre côté,
     par la règle 4.
     Si c'est un b qui est produit à gauche (par la règle 3) le non-terminal E s'en va pondre un b
     par la règle 5.
     De cette façon, le premier mot est construit lettre à lettre par l'action du digramme non-terminal AB
     (règles 2 et 3), le non-terminal C marque "la fin du chantier" où sont déposés les matériaux fournis
     par les règles 4 et 5. Le moment venu, A, B et C disparaissent par les règles 10 et 11.
     
     

   • Exercices

     Vérifier que la grammaire suivante engendre {aibjck | 1≤ i ≤ j ≤ k}
     
     
     1. S -> aTbX 
     2. S -> abX
     3. T -> aTbC
     4. T -> TbC 
     5. T -> TC 
     6. T -> bC 
     7. T -> C
     8. Cb -> bC
     9. CX -> Xc
     10. X -> c
     
     et que la suivante engendre {w ∈ {a, b, c}* | #(a) = #(b) = #(c)},
     où "#(a)" désigne le nombre d'occurrences de la lettre a dans le mot w, etc.
     Il s'agit donc des mots qui contiennent autant d'occurrences de a que de b et que de c.
     
     
     1. S -> ABC
     2. S -> ABCS
     3. AB -> BA
     4. AC -> CA
     5. BC -> CB
     6. BA -> AB
     7. CA -> AC
     8. CB -> BC
     9. A -> a
     10. B -> b
     11. C -> c
     
     Quel est le langage engendré par celle-ci ?
     
     
     1. S -> AB
     2. A -> aAX
     3. A -> aX
     4. B -> bBd
     5. B -> bYd
     6. Xb -> bX
     7. XY-> Yc
     8. Y -> ε

     
     

5. Automates linéairement bornés (en anglais linear-bounded automata)

   • Principe

     La classe d'automates associée aux grammaires CS est celle des machines de Turing auxquelles on impose
     que la quantité de mémoire utilisée par le calcul (la longueur de bande nécessaire) ne croisse que de manière linéaire
     avec la longueur du mot donné (et non pas de manière quadratique ou - pire - exponentielle).
     On notera que cette contrainte sur la quantité de mémoire utilisée ne dit rien sur le temps de calcul,
     qui peut être arbitrairement grand.
     
     En français courant, cela signifie qu si le mot-candidat et de longueur n,
     le nombre de cases utilisées sur la bande de travail de l'automate ne doit pas dépasser kn
     (et non kn²...) pour un certain coefficient fixe k.
     
     Par exemple, pour décider si le mot candidat a bien la propriété " #(a) = #(b) = #(c)",
     l'automate peut lire le mot de gauche à droite, à chaque lettre qu'il lit, retourner poser une marque à gauche du mot
     de manière à constituer 3 compteurs, à la fin de la lecture retourner faire les comptes pour déterminer si
     l'égalité est vérifiée. Pour cela il n'aura besoin que d'un espace supplémentaire de la même longueur que le mot candidat.
     Dans ce cas, le coefficient k vaudra 2.
     

   • Exemple

     Wikipedia cite l'exemple suivant :
     

     An example of a context-sensitive language that is not context-free is L = { a^p : p is a prime number }.
     L can be shown to be a context-sensitive language by constructing a linear bounded automaton which accepts L.

     On imagine bien, en effet, que pour déterminer si un mot a pour longueur un nombre premier, une machine de Turing
     peut se débrouiller sans sortir d'une copie de ce mot - avec force va-et-vient sans doute, pour déterminer si le mot peut être découpé
     en parties égales de toutes les longueurs inférieures, mais sans devoir emmagasiner d'information en dehors de cette plage.
     Quant à écrire la grammaire correspondante...
     

   • Non-exemple

     Le même article de Wikipedia ajoute :
     

     An example of recursive language that is not context-sensitive is any recursive language whose decision is an EXPSPACE-hard problem,
     say, the set of pairs of equivalent regular expressions with exponentiation.

     Par recursive language, entendez "langage pour lequel il existe une machine de Turing qui résout son problème des mots".
     Il s'agit donc d'exhiber un langage qui n'est pas CS - chose notoirement difficile, vu que n'importe quelle définition compréhensible
     par le commun des mortels a de fortes chances de décrire un problème soluble par la mécanique CS.
     
     En l'occurrence, il s'agit du langage formé des couples d'expressions régulières,
     
     • écrites avec les trois opérateurs classiques union, produit, étoile
     • auxquels on ajoute l'opérateur "élever au carré" : au lieu du produit "e.e" on autorise à écrire "e2",
     • et qui représentent le même langage régulier.
       
       
     Par exemple, les savants calculs que nous avons faits au cours n° 2 montrent que le mot
     

     yx*xy*x=yx2x*∪yxyy*x∪yx2x*yy*x

     fait partie de ce langage.
     
     Albert Meyer & Larry Stockmeyer, du MIT, ont montré en 1972 que
     pour déterminer si deux e.r. de ce type (avec l'opérateur supplémentaire "carré") décrivent ou non le même langage régulier,
     on a besoin d'un espace-mémoire qui croît exponentiellement avec la taille de la donnée (la longueur des deux expressions).
     Il n'est donc pas question de reconnaître notre langage avec un automate linéairement borné !
     
     Mais pourquoi ne pas se contenter des expressions régulières ordinaires (sans l'opérateur "carré") ?  
     Le problème de leur équivalence exige un espace qui croît de manière polynômiale (il est PSPACE-complet) n'est-ce pas assez ?
     Le rôle de l'opérateur "carré" est apparemment de faire croître de manière exponentielle la longueur de l'e.r. ordinaire
     équivalente [car "x porté n fois au carré" s'écrit en longueur n+1 et représente en notation ordinaire une chaîne de 2ⁿ fois x],
     ce qui fait passer le problème de la classe PSPACE à la classe EXPSPACE. N'est-ce point de l'overkill ?