Règles sans contexte
-
Définition
Une grammaire context-free est une grammaire dont toutes les règles sont de la forme
A -> w
oùAest un symbole non-terminal etwun mot quelconque.
On note deux différences par rapport aux grammaires context-sensitive :
- l'absence de contexte dans le membre gauche :
Dans le modèle context-sensitive, on interprète une règle du genreuAv -> uwvcomme "le non-terminal
Ase réécrit enwdans le contexte (u,v)".
Dans le modèle context-free, on dira que
"le non-terminalAse réécrit enwindépendamment du contexte où il apparaît".
On voit donc que l'adjectif anglais free doit être traduit en français non point par libre,
mais par affranchi, libéré, ou même franc au sens que ce mot avait chez Ronsard :
Franc des liens du corps pour n'estre qu'un esprit.
- l'absence de contrainte sur le membre droit :
Le modèle context-sensitive exige quewsoit non-vide, pour assurer le caractère "non-contractant"
de ses règles.
Le modèle context-free n'a que faire de cette précaution !
Il s'ensuit que stricto sensu la classe des langages CF n'est pas incluse dans celle des langages CS,
alors que le modèle CF est de toute évidence une particularisation de CS où tous les contextes sont vides.
Pour éviter cette absurdité, les définitions officielles de CS (Wikipedia...) ajoutent des règles spéciales S -> ε.
Nous négligeons ces détails de présentation.
- l'absence de contexte dans le membre gauche :
-
Exemples
- Les langage des systèmes bien parenthésés est engendré
par la grammaire
S -> SSS -> εS -> (S)S -> [S]S -> {S}S -> <S>
vues au cours n° 17 : pour notre exemple favori le mot "([]{<<>>}([(){<>}]))", en dérivant "à gauche"
S-3>(S)-1>(SS)-4>([S]S)-2>([]S)-1>([]SS)-5>([]{S}S)-6>([]{<S>}S)-6>([]{<<S>>}S)-2>([]{<<>>}S)
-3>([]{<<>>}(S))-4>([]{<<>>}([S]))-1>([]{<<>>}([SS]))-3>([]{<<>>}([(S)S]))-2>([]{<<>>}([()S]))
-5>([]{<<>>}([(){S}]))-6>([]{<<>>}([(){<S>}]))-2>([]{<<>>}([(){<>}]))
On aurait pu aussi bien dériver "à droite" :S-3>(S)-1>(SS)-3>(S(S))-4>(S([S]))-1>(S([SS]))-5>(S([S{S}]))...
- Le langage {
anbn|n>0} est engendré par
S -> aSb
S -> ab
- Le langage des palindromes {
ww~|w∈X*}
S -> εS -> aSaS -> bSb
- Le langage des mots contenant autant de
aque deb:
S -> SSS -> aSbS -> bSaS -> ε
On observe que tout mot w contenant autant deaque debse décompose (d'une manière unique) en facteurs de la forme
auboubva, où u et v contiennent autant deaque deb: ces facteurs correspondent aux passages par 0 de la fonction
(nombre dea- nombre deb). Exemple : pour le motaabaababbbbbbaabaaba
aabaababbb b b b a a b aa ba -> a abaababb b / b bbaaba a / ba
1212323210-1-2-3-2-1-2-10-10
Les facteurs en question sont engendrés par les règles 2, 3, 4. La règle 1 se charge de les concaténer.
Par exemple, le mot en question sera engendré par (en dérivant à gauche):
S-1>SS-1>SSS-2>aSbSS-2>aaSbbSS-1>aaSSbbSS-1>aaSSSbbSS-3>aabSaSSbbSS-4>aabaSSbbSS-2>
aabaaSbSbbSS-4>aabaabSbbSS-2>aabaabaSbbbSS-4>aabaababbbSS-3>aabaababbbbSaS-3>aabaababbbbbSaaS
-1>aabaababbbbbSSaaS-3>aabaababbbbbbSaSaaS-4>aabaababbbbbbaSaaS-2>aabaababbbbbbaaSbaaS
-4>aabaababbbbbbaabaaS-3>aabaababbbbbbaabaabSa-4>aabaababbbbbbaabaaba
- Les langage des systèmes bien parenthésés est engendré
par la grammaire
-
Non-exemples
-
Lemme de la double étoile (en anglais pumping lemma)
Soit L un langage CF infini.
Dans tout mot w de L suffisamment long on peut trouver deux facteurs u et v dont l'un au moins n'est pas vide,
w = fugvh ∈ L
tels que, pour tout entier n, on ait fungvnh ∈ L.
Idée de la preuve :
le mot w ∈ L étant arbitrairement long, la chaîne de réécritures qui l'engendre est aussi arbitrairement longue ;
[plus précisément, il existe une branche de l'arbre de dérivation - cf. cours 16 - qui est arbitrairement longue]
par conséquent il y a au moins un symbole non-terminalT
- qui apparaît deux fois dans cette chaîne [branche],
- et qui entre ces deux apparitions apporte une
contribution non nulle au mot terminal
S->* fTh ->* fuTvh ->* fugvh = w∈ L, avec la contribution uv non vide.
D'où il suit queT->* uTv et queT-> g, doncT->* ungvn pour tout entier n,
et puisqueS->* fTh,S->* fungvnh, c'est-à-dire que fungvnh∈ L pour tout entier n.
Quod erat demonstrandum.
- qui apparaît deux fois dans cette chaîne [branche],
-
Exemples
Aucun des exemples de langages CS que nous avons vus au cours 17 n'est CF.
- {
anbncn|n>0} parce que l'itération simultanée ne concerne que deux facteurs, pas trois !
on ne pourra donc pas maintenir l'égalité sur les troisa,betcsimultanément.
De même pour {aibjck | 1≤ i ≤ j ≤ k}, et a fortiori, pour {anbncndn | n>0} !
- Le langage des carrés {ww
| w ∈
{
a,b}*} demande un peu plus d'attention. Appelons-le L.
En particulier, il faut un argument qui ne s'applique pas aux palindromes !
On examine les mots de L qui sont de la formeapbqarbsavec p, q, r, s positifs.
(en d'autres termes, on prend l'intersection de L avec le langage réguliera+b+a+b+, voir ci-après).
Les mots en question sont de la formeanbmanbmavec m et n positifs.
L'idée est que la mécanique CF est incapable de maintenir l'égalité à la fois sur lesaet sur lesb.
Pour le montrer on a besoin d'une forme plus forte du lemme précédent, qui précise que le "facteur itérant"
ugv a une longueur bornée. Soit p la borne en question : choisissons m et n > p.
Alors le facteur itérant doit être logé
- soit dans les
adu début, ce qui ruine l'équilibre avec lesade la deuxième moitié - soit à cheval sur les
aet lesb, ce qui détruit la structure de "carré" ww - soit dans les
bde la première moitié, ce qui ruine l'équilibre avec lesbde la deuxième moitié - etc.
- soit dans les
- {
-
-
Propriétés de fermeture de la classe des langages CF
-
Union
Soient G1 et G2 deux grammaires CF engendrant deux langages L1 et L2, sur le même alphabet terminal.
Les deux ensembles de symboles non-terminaux peuvent sans inconvénient être supposés disjoints.
Il suffit pour engendrer l'union L1∪L2 de prendre la grammaire G ainsi construite :
- ses symboles non-terminaux sont ceux de G1,
ceux de G2 et un
nouvel axiome
S - ses règles sont celles de G1,
celles de G2 et
deux nouvelles règles :
S->S1, S->S2
oùS1etS2sont les axiomes de G1 et de G2 .
- ses symboles non-terminaux sont ceux de G1,
ceux de G2 et un
nouvel axiome
-
Produit
Même raisonnement en remplaçant L1∪L2 par L1L2, et les "deux nouvelles règles :S->S1, S->S2"
par "une nouvelle règle :S->S1S2".
-
Étoile
Même raisonnement avec une seule grammaire G1, en remplaçant L1L2 par L1*,
et "une nouvelle règle :S->S1S2" par "deux nouvelles règles :S->S1S, S->ε". -
Intersection avec un langage régulier
L'intersection de deux langages CF n'est pas CF en général !
Contre-exemple :
- L1 = {
anbncp|n>0,p>0} est CF (produit de {anbn|n>0} parc+) - L2 = {
apbncn|n>0,p>0} est CF (produit dea+ par {bncn|n>0} ) - L1∩L2
= {
anbncn|n>0} qui n'est pas CF.
Toutefois, l'intersection d'un langage CF avec un langage régulier est CF.
Il n'est pas très facile de le démontrer au moyen d'une grammaire.
En revanche, le résultat sera évident quand nous mettrons en marche les automates à pile,
qui sont les correspondants des grammaires CF du côté des automates.
Munis de ce résultat, nous pouvons revisiter la preuve que le langage des carrés n'est pas CF
comme suit : considérons l'intersection {ww | w ∈ {a,b}*}∩a+b+a+b+: si le premier langage est CF,
l'intersection l'est aussi. Or cette intersection est exactement {anbmanbm| m >0, n>0}.
Il ne reste plus qu'à démontrer que ce dernier langage n'est pas CF, ce qui se fait par le même argument
que ci-dessus, un tantinet simplifié.
- L1 = {
-
Automates à pile
-
Idée générale
La contrainte qui définit les automates à pile (en anglais pushdown automata) est de n'utiliser leur mémoire
qu'en se conformant aux règles suivantes (qui, en informatique, définissent la structure de pile - en anglais stack ou pushdown stack) :
- la lecture n'est possible qu'au sommet de la pile (
top)
- pour prendre connaissance des informations qui sont situées au dessous du sommet,
il faut détruire ce qui se trouve par-dessus (pop) jusqu'à ce que l'information désirée apparaisse au sommet - l'écriture n'est possible qu'en ajoutant un information
sur le sommet de la pile (
push)
- cette information se trouve alors au sommet - on ne peut pas lire sur une pile vide (
empty).
top,pop,pushetemptyrésument le comportement de pile.
Voici un schéma emprunté à Wikipedia , où le lecteur soucieux d'exactitude trouvera des définitions en forme.
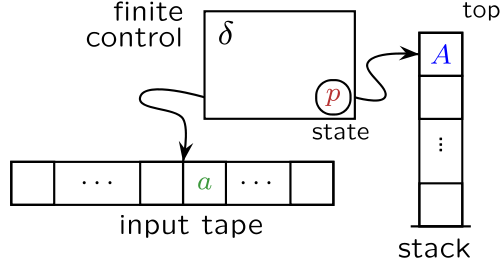
La "contrainte de pile" est une contrainte très forte.
Pourtant, il n'est pas évident qu'elle implique une croissance linéaire de la consommation de mémoire.
En effet, la définition générale stipule que l'automate est non-déterministe :
lisant une lettrexsur sa bande d'entrée, voyant un symbolepau sommet de sa pile, se trouvant dans un états,
l'automate choisit d'avancer ou non sa lecture, d'empiler un autre symbolepush(q)ou au contraire d'écrêter sa pilepop(),
et de passer dans un étattou dans un autre...
Dans ces conditions, qu'est-ce qui l'empêche d'empiler une quantité exponentielle d'informations et d'en faire bon usage ?
Il y a là un point de finesse à éclaircir.
En tout état de cause, il est clair qu'en faisant fonctionner en parallèle un automate fini et un automate à pile
on obtient un nouvel automate à pile (dont le "contrôle fini" a été perfectionné, mais dont la gestion de pile n'a pas changé).
C'est ce qui permet d'affirmer, comme nous l'avons fait précédemment, que l'intersection (= fonctionnement en parallèle)
d'un langage CF (= automate à pile) avec un langage régulier (= automate fini) est encore CF. - la lecture n'est possible qu'au sommet de la pile (
-
Les deux modèles pour l'acceptation
La tradition a retenu deux types de comportement pour accepter ou rejeter un mot-candidat : par état terminal et par pile vide.
- par état terminal : comme pour un
automate fini, on désigne un sous-ensemble de l'ensemble (fini) des
états,
et le mot est accepté si, et seulement si, il existe un calcul de l'automate lisant ce mot et s'achevant dans un des états désignés.
Dans ce cas le contenu de la pile en fin de calcul est sans importance.
- par pile vide : le mot est accepté
si, et seulement si à la fin du calcul la pile est vide.
et par des artifices variés on montre que ces deux formules sont équivalentes quant à la classe des langages reconnus.
Exemples : le langage des systèmes bien parenthésés est facilement reconnu par un automate déterministe avec pile vide.
En revanche, un langage comme le produita*{anbn|n>0} = {ambn|m>=n>0} sera plus naturellement reconnu
par un automate déterministe avec un état final attestant qu'après avoir lu desbon n'a pas rencontré de nouveau desa.
Nous verrons apparaître des automates à pile très précisément décrits quand nous étudierons l'analyse syntaxique,
il est donc inutile de nous embarrasser d'une définition formelle ici. - par état terminal : comme pour un
automate fini, on désigne un sous-ensemble de l'ensemble (fini) des
états,
-
La question du déterminisme
Contrairement à ce qui se passe pour les automates finis, il n'est pas possible en général de trouver
un automate à pile déterministe qui reconnaît le même langage qu'un automate à pile non-déteriniste donné.
L'exmple classique en la matière est le langage des palindromes {ww~} :
le fonctionnement de l'automate à pile reconnaissant ce langage est très simple :
- au fur et à mesure de sa lecture du mot-candidat, il empile les lettres qu'il lit.
- parvenu au milieu du mot, il change d'état et décide de
vérifier la palindromité
en s'assurant que désormais chaque lettre qu'il lit est identique à celle qu'il trouve au sommet de sa pile - et l'élimine aussitôt.
mais comment savoir qu'on est au milieu du mot ?
Hiérarchie de Chomsky
Chomsky, Noam (1956). "Three models for the description of language". IRE Transactions on Information Theory (2): 113–124.L'article original est accessible en pdf sur Wikipedia.
- "Type 0" (grammaires générales - machines de Turing),
- "Type I" (grammaires CS - automates linéairement bornés),
- "Type II" (grammaires CF - automates à pile),
- "Type III" (grammaires linéaires unilatères - automates finis)
-
Grammaires linéaires
Une grammaire CF est linéaire si chaque membre droit de règle contient au plus un symbole non-terminal.
Exemples : sur les quatre exemples de grammaires CF que nous avons vues ci-dessus, les n°s 2 et 3 sont linéaires.
Cette terminologie renvoie à l'interprétation des grammaires CF comme des équations algébriques portant sur des langages :
La grammaire de l'exemple n° 4 :
S -> SSS -> aSbS -> bSaS -> ε
S = SS ∪ aSb ∪ bSa ∪ e(avec les abus de notations habituels).
Cette équation sera dite quadratique par les algébristes, en raison de la présence du carré "SS".
Au contraire, l'équationS = aSb ∪ abqui traduit la grammaire de l'exemple n° 2
S -> aSbS -> ab
Sn'y apparaît qu'au premier degré
- le mot "linéaire" dans le langage des mathématiciens renvoyant au fait que
la fonction du premier degré y = ax + b est représentée par une ligne droite.
Dans une grammaire linéaire, la distinction entre dérivation droite et dérivation gauche disparaît,
les arbres de dérivation sont des chaînes, et la question de l'ambiguïté ne se pose pas.
Si on impose à une grammaire linéaire que l'unique non-terminal du membre droit soit tout à droite (ou tout à gauche)
cette grammaire devient linéaire unilatère.
Par exemple :
S -> yAA -> xAA -> xBB -> yBB -> x
Un couple de règles unilatères mais en sens contraire commeS->xA,A->Syconduit àS ->* xSy,
qui sort de l'épure comme on va le voir.
-
Grammaires linéaires unilatères et langages réguliers
La classe des langages engendrés par les grammaires linéaires unilatères est exactement la classe des langages réguliers.
La raison en est qu'une grammaire linéaitre unilatère n'est qu'une autre manière d'écrire un automate fini (non-déterministe).
En effet, dans un dérivation d'une grammaire linéaire unilatère, il y a à chaque pas un seul non-terminal à droite,
que l'on peut interpréter comme dénotant l'état de la dérivation.
Ainsi, avec la grammaire ci-dessus, la dérivation :
S -> yA -> yxA -> yxxA -> yxxxB -> yxxxyB -> yxxxyyB > yxxxyyx
peut se lire comme le calcul pour le mot d'entréeyxxxyyxd'un automate fini non-déterministe
- dont les états sont
S(initial),AetB - avec pour transitions
s(S,y)=A,s(x,A)= {A,B} (non-déterminisme),s(B,y)=B, - et enfin
s(B,x)est l'unique état terminalT(qu'il faut adjoindre à {S,A,B}).
valeur de l'expression régulièreyx*xy*x.
Voici les termes de la correspondance :
- non-terminaux de la grammaire <--> états de l'automate
- axiome de la grammaire <--> état initial de l'automate
- règles non-terminales de la grammaire <--> transitions de l'automate
- règles terminales de la grammaire <--> transitions de l'automate vers un état terminal
- dérivation d'un mot terminal à partir de l'axiome
<--> calcul de l'automate pour ce mot,
partant de l'état initial et arrivant à un état terminal.
N.B. En toute rigueur, il faut d'abord "normaliser" la grammaire pour n'avoir que des lettres dans les règles, et non des mots composés
(avec des non-terminaux supplémentaitres).
- dont les états sont
-
Exercice :
écrire des grammaires linéaires unilatères (à gauche ou à droite, selon vos convictions politiques)
- pour les automates finis
- pour les expressions régulières