Cours n° 6, 22 novembre 2011
Tout langage reconnaissable par un automate fini est
régulier
Théorème de Kleene
- Construction
d'un automate reconnaissant le langage donné par
une e.r.
- Premier
exemple
- Second
exemple, où apparaît l'opérateur d'union
- Réciproquement,
construire une e.r. pour le langage reconnu
par un automate fini
- L'algorithme
de McNaughton & Yamada
Une telle construction découle des résultats du cours n°6, qui donnent
pour les 3 opérations union, produit et étoile,
trois procédés pour construire un automate reconnaissant leur résultat
à partir des automates reconnaissant leurs opérandes.
D'autre part, le logiciel automate (dans son étape de compilation) propose par défaut un procédé (dit algorithme de Thompson),
que nous allons examiner ici.
-
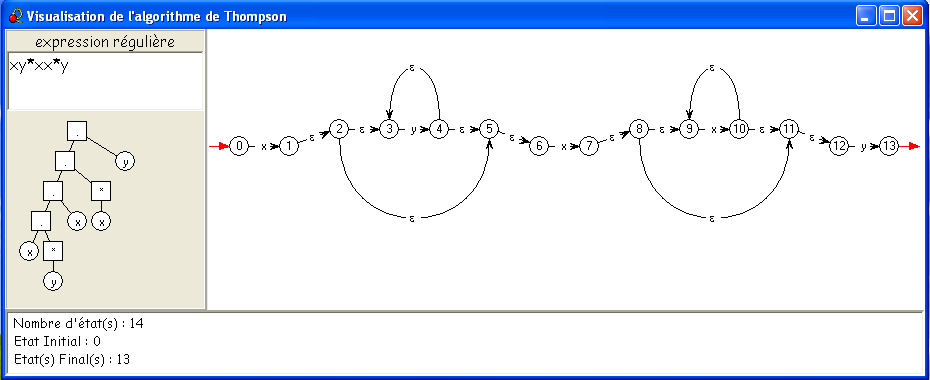
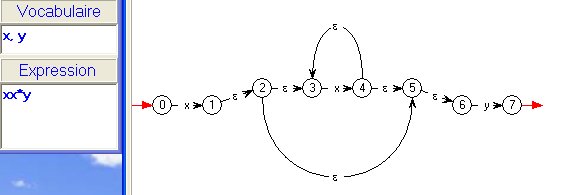
Ce procédé donne donne pour l'expression
xy*xx*y :
Pouvons-nous interpréter ce croquis ? Complètement !
- La transition 0 -> 1 par la lettre
x
correspond à l'automate minimal reconnaissant le singleton {x},
avec 1 terminal.
- La transition 3 -> 4 par la lettre
y
correspond à l'automate minimal reconnaissant le singleton {y},
avec 4 terminal.
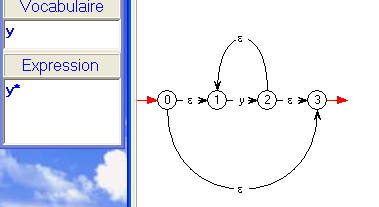
- Le sous-automate formé par les états 2, 3, 4 est donc
exactement ce que nous aurions construit pour reconnaître
y*,
à ceci près que la construction de Thompson ajoute un état terminal
unique atteint par des ε-transitions à partir de "nos" états terminaux.
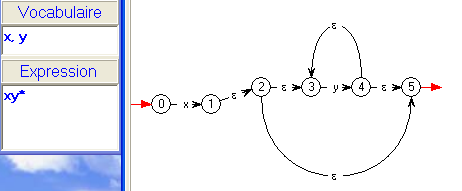
- L'ε-transition 1 -> 2 est donc bien celle qui
est
prévue pour reconnaître le produit
xy*.
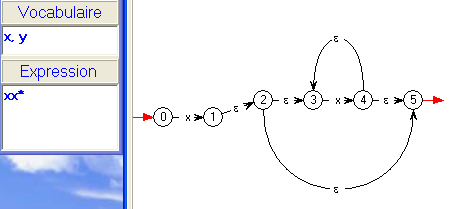
- De même, le sous-automate formé par les états 6 à 10
est
exactement ce que nous aurions construit pour reconnaître
xx*.
- Et la transition 12 -> 13 par la lettre
y
correspond à l'automate minimal reconnaissant le singleton {y}.
et le sous-automate de 8 à 13 reconnaît donc xx*y.
Nous voyons donc que l'algorithme de Thompson n'est pas très différent
de l'application systématique des procédés vus au cours 5
- du moins, en l'absence de l'opération d'union, car là il suit
vraiment une autre voie.
-
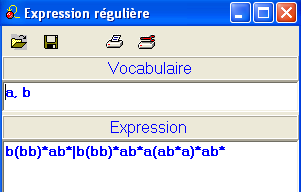
Nous reprenons notre exemple scolaire : en notation
acceptable par le logiciel automate :
(aa|b)*ab(bb)*
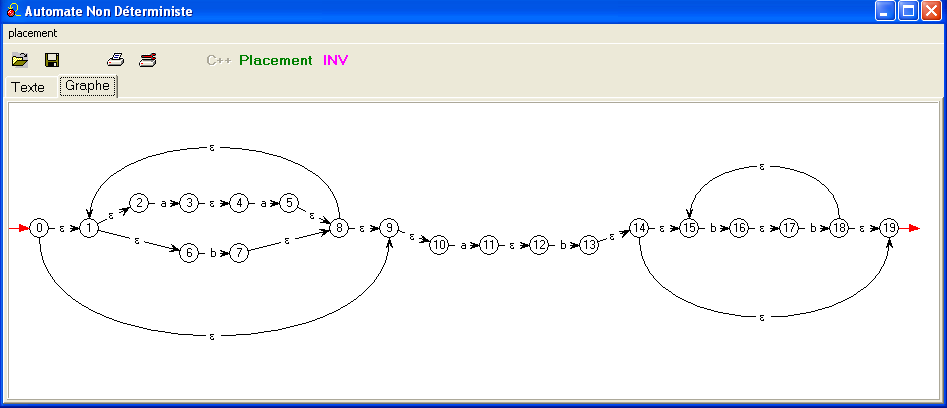
C'est dans la partie 0-9 que se situe la nouveauté.
- À partir de {
aa}:
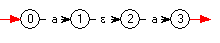 et de {
et de {b}
: 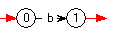
le logiciel construit {aa}∪{b}
: 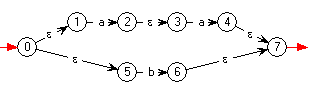
qui n'est pas du tout ce que prévoit le cours 5 !
- Pas de produit direct des ensembles d'états, mais
- leur réunion,
- deux transitions spontanées d'un nouvel état
initial
vers les deux étatis initiaux,
- un unique état terminal atteint par deux
transitions spontanées depuis les états terminaux.
Bref un automate non-déterministe... et pourquoi pas ?
Dans la mesure ou toute la construction se fait avec du
non-déterminisme, sans chercher à déterminiser et à réduire à chaque
pas,
ce procédé se justifie !
- La suite de la construction suit les mêmes lignes que
notre premier exemple.
Si nous y arrivons, nous aurons montré l'équivalence entre les deux
propriétés être la valeur d'une e.r. et être
reconnu par un automate fini,
équivalence due au grand logicien américain S.
C. Kleene en 1956.
Il y a plusieurs méthodes pour effectuer cette construction, qui sont
plus ou moins efficaces.
Nous présentons ici la plus directement intuitive...
Le langage reconnu par l'automate est la réunion (finie) des langages
obtenus en prenant un seul état terminal à la fois.
Notre automate ayant n états, nous nous concentrons donc sur la
construction d'une e.r. pour chacun
des n×n
langages
Ls,s' = { w∈X*
| s.w = s' }
formé de tous les mots qui envoient un état s
quelconque sur un autre état s'.
Si nous y parvenons, le langage reconnu par l'automate sera la valeur
d'une réunion finie d'e.r., donc d'une e.r.
L'idée est de procéder pas à pas en prenant en compte un nombre
croissant d'états intermédiaires entre s et s'.
Les états étant supposés numérotés de 0 à n, on
commence par aucun état intermédiaire, puis
seulement s0, puis s0
et s1, puis s0, s1
et s2, etc.
Le logiciel automates propose une visualisation très parlante de ce
processus.
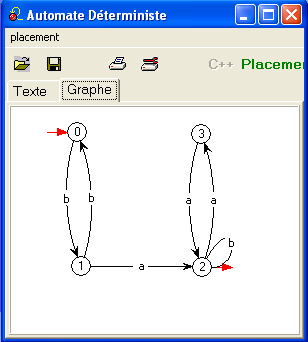
La voici sur la base de l'automate "renversé minimal" que nous avons vu
au cours 6.
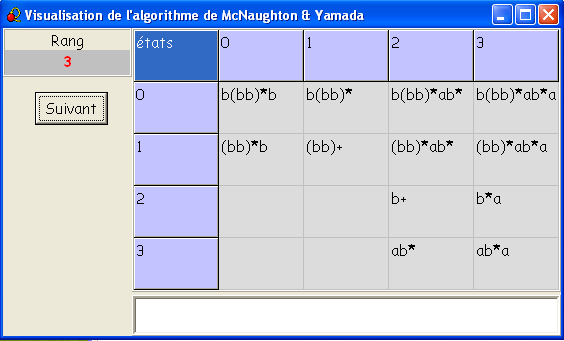
On représente les 4×4 e.r. en construction par un tableau à double
entrée : la case (ligne i, colonne j)
contient l'e.r. des mots qui envoient si
sur sj
en passant pas les états intermédiaires autorisés par l'étape en cours.
Quand la case est vide le langage l'est aussi.
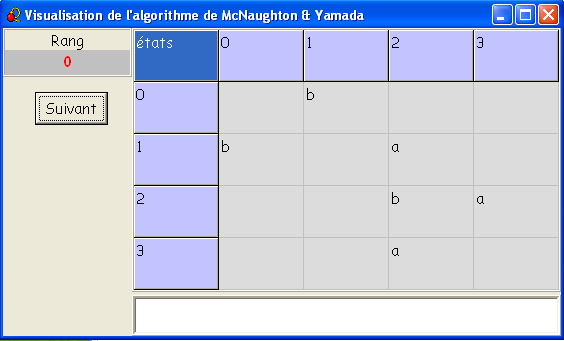
- L'étape 0 correspond aux calculs qui ne passent par aucun
état intermédiaire : c'est-à dire aux
transitions elles-mêmes.
- L'étape 1 correspond aux calculs
qui ne passent que par l'état 0.
Par rapport à l'étape 0, on voit seulement apparaître l'aller-retour
1-0-1 provoqué par le mot bb.
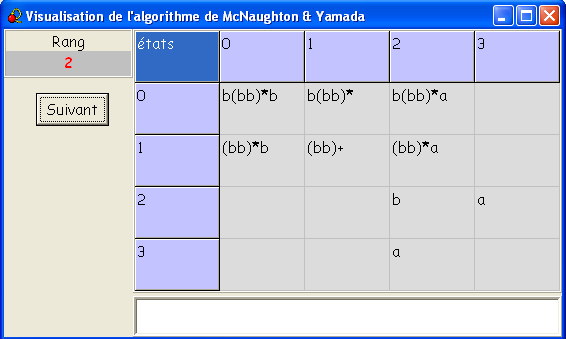
- L'étape 2 correspond aux calculs
qui ne passent que par les états 0 et 1.
On voit fleurir les (bb)* :
on peut en effet tourner indéfiniment autour de 1.
À noter que le mot vide n'est pas pris en compte, d'où (bb)+
et non (bb)* pour 1-1.
- L'étape 3 correspond aux calculs
qui ne passent que par les états 0, 1 et 2.
On voit apparaître la boucle sur 2 par b,
qui est aussitôt distribuée.
En effet, d'une manière générale, on calcule l'e.r. de l'étape 3 en
fonction des e.r. de l'étape 2 comme suit :
Soit Es,s'
l'e.r. décrivant les chemins de s à s'
à l'étape 2, et Fs,s'
l'e.r. décrivant les chemins de s à s'
à l'étape 3.
Fs,s'
= Es,s' ∪
Es,2 (E2,2)*E2,s'
, puisque pour aller de s à s'
en ne passant que par 0, 1 et 2,
- soit on ne passe pas par 2, donc le chemin est
dans Es,s'
- soit on passe par 2, donc
- on y va une première fois par un chemin qui est
dans Es,2
,
- on décrit un circuit autour de 2 qui est dans E2,2,
circuit que lon répère jusqu'à ce que ...
- on quitte 2 une dernière fois par un chemin qui est
dans E2,s'
.
Ce raisonnement est général et vaut pour toutes les étapes.
- L'étape 4 correspond aux calculs de s à
s'
qui ne passent que par les états 0, 1, 2 et 3, c'est-à-dire à tous
les calculs.
Et par conséquent l'e.r. cherchée peut être affichée.
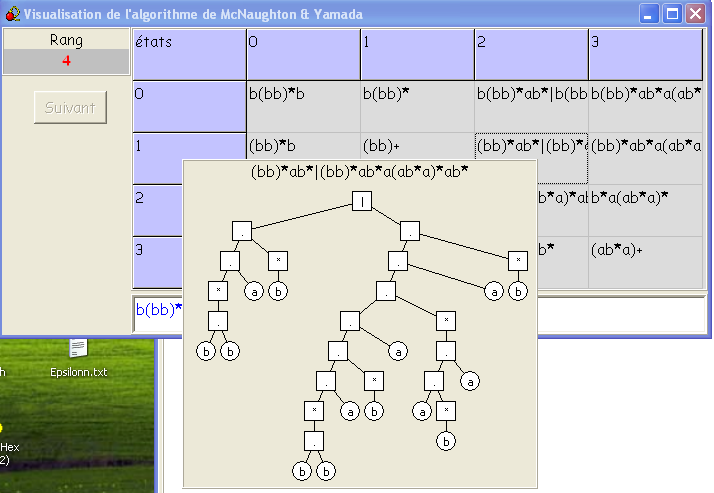
Comme certaines expressions sont trop longues pour s'écrire dans leurs
cases - le logiciel offre une visualisation améliorée
obtenue en cliquant dans la case que l'on veut examiner :
- Et à la fin du calcul, le résultat officiel !
Est-il évident que notre estimation précédente [fondée sur le
renversement de (aa|b)*ab(bb)*]
et ce résultat donné par la machine ont bien la même valeur ?
C'est-à-dire, que (bb)*ba(aa|b)*
= b(bb)*ab*|b(bb)*ab*a(ab*a)*ab*
?
On a (bb)*ba = b(bb)*a,
reste donc à démontrer que b(bb)*a(aa|b)*
= b(bb)*ab*|b(bb)*ab*a(ab*a)*ab*
c'est-à-dire que (aa|b)* =
b*|b*a(ab*a)*ab*
:
- l'inclusion de droite dans gauche est facile : à droite
les
a
vont toujours par 2 ;
- l'inclusion de gauche dans droite est moins évidente :
tout mot w de (aa|b)*
qui contient au moins un a
en contient au moins 2,
il peut donc se factoriser en marquant le premier et le dernier a,
soit w = bpafabq
;
comme le premier a
est suivi d'un a, et que
le dernier a est
précédé d'un a, le facteur
médian f, s'il n'est pas vide,
doit être de la forme aga
; si f est vide, ou si g ne
contient point de a, le
mot w est bien dans le membre droit.
Si g contient des a,
ceux-ci vont par 2, et en marquant la première occurrence g
se factorise en g = braah.
Si h ne contient point de a,
f est de la forme aga
= abraabsa
et le mot w est bien dans le membre droit.
Si h contient des a,
le même raisonnement s'applique : on peut donc procéder par récurrence
sur la longueur de w.
Doutez-vous à présent de l'intelligence des machines ?


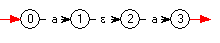 et de {
et de {